Bstをclassで作ろう
このワークシートはMath by Codeの一部です。
2分探索BS
2分探索木BST
1.2分探索
<2分探索>
データがソートされているとき、
探し物があるときに2分探索はとても便利だということは
だれでも経験があるでしょう。
上か下かで調べる対象が
半分になっていくというやつですね。
N個数を半分にしていくときに最悪で何回半分にするのかが調べる回数になるね。
たとえば、3回調べて見つかるとしたら,N=23
となる。言い換えると3=log2Nだね。
だから、調べる回数はlogNのレベルだということだ。
もしもNが1024だとしたら、2^10=1024だから、log1024=10だ。
前から順にさがして最悪1024回調べるところが、2分探索ではわずか最悪10回ですむ。
調べる回数が100分の1のレベルに激減するね。
すばらしい!
2.2分探索木(BST)
2分探索BinarySearch, BSはデータはソートされているだけだったが、
ソートするという手間がかかっているからこそ、検索が楽にできた。
では、2分探索という発想がそのままデータ構造になるとすごく便利になりそうだね。
それが、2分探索木BinarySearchTree(BST)だ。
BSTは親から左の部分木が親より小さく、親から右の部分木が親より大きく、これがどの点を親にしても
成り立つ。
だから、BSTそのものがソートをされたデータを表していることになる。
データxを追加するときは親と比べて大きかったら右の部分木に進み、親より小さかったら左に進む。
これを続けていけば、いつかは行き先が決まる。
データ検索も、データ削除も同じ要領でできるはずだね。
質問:pythonでBSTを実装するにはどうしたらよいでしょうか。
BSTの最小単位は左木と右木とデータをもつ頂点ですね。
その3つのデータ(left, right,data)をもつ頂点を定義しよう。
たいていはnodeという名前で定義されている。
しかし、ただの点・節ではなく2分木の最小単位なので「BT」とした。
BSTはBTがrootから順々に下に伸びているものだね。
1件追加する関数insert(data)は行き先を探して見つかったらBTを値としてセットするものだ。
根rootが空なら、root=BT(data)とセットする。
空でないなら再帰的に今いるv.dataより入れたいnew_v.dataが小さいとv.leftへ,
大きいならv.leftへ登録しよう。
あとで、追加状態の確認ができるように、
左に追加したら、print(f"{new_v.data} <={v.data}")
右に追加したら、print(f"{v.data}=> {new_v.data}")
とすることで、木の登録状況の確認ができるね。
1件ずつ追加するのは大変だから、
リスト渡しでinsert(data)をくり返してくれる関数
make_from(lst)を作ろう。
1件追加と同様のロジックで関数seach(data)も作ろう。
#[IN]Python
#2分する頂点クラスBT==========================
# dataと左枝と右枝を持つデータ構造(dataは大小判断ができれば何でもよい。)
class BT:
def __init__(self, data):
self.left = None
self.right = None
self.data = data
#2分探索木のクラスBST==========================
# rootから順にBT(data)を入れる。
# rootを含む各点vで、v、v.left、v.rightにBT(data)のデータを入れ続けられます。
class BST:
def __init__(self):
self.root = None
# リストから作る。
def make_from(self, lst):
for item in lst:
self.insert(item)
# 1件追加
def insert(self, data):
# vにBTデータをvに入れる。
# vといえば、BTデータとして読んでください。
v = BT(data)
if self.root is None:
self.root = v
else:
self._insert_recursive(self.root, v)
def _insert_recursive(self, v, new_v):
if new_v.data < v.data:
if v.left is None:
v.left = new_v
print(f"{new_v.data} <={v.data}")
else:
self._insert_recursive(v.left, new_v)
elif new_v.data > v.data:
if v.right is None:
v.right = new_v
print(f"{v.data}=> {new_v.data}")
else:
self._insert_recursive(v.right, new_v)
else:
print(f"データ{v.data}が重複しています。")
# 1件探す
def search(self, data):
return self._search_recursive(self.root, data)
def _search_recursive(self, v, data):
if v is None:
return False
if data == v.data:
return True
elif data < v.data:
return self._search_recursive(v.left, data)
else:
return self._search_recursive(v.right, data)
myBST=BST()
nums = [20,30,40,5,10,15,25,35]
myBST.make_from(nums)
#===============================
[OUT]
20=> 30
30=> 40
5 <=20
5=> 10
10=> 15
25 <=30
35 <=40
3.BSTの視覚化
BSTを文字で表示しても、正しく登録されたかどうかだけしかわかりません。
グラフを使って、全体としての大小関係や全体として左右のバランスが見えるようにしたい。
質問:どうすれば、BSTのデータからグラフができるでしょう。
BSTにBTつないで、printしている部分を変えることを考えよう。
グラフオブジェクトを宣言して、
print(f"親=>子")、print(f"子<=親")の部分を
G.edge(親,子,label=左/右)
のようにかきかえて
そのつど矢印と左か右かのラベルを登録してもよいかもしれない。
しかし、グラフは表示されるが問題がある。それは、登録した順に矢印が書かれるからだ。
左L,右rが正しくかかれていても、登録順が右が先で、左が後だと、左側にLの辺が、右側にrの辺が表示
されてしまう。
これでは、数が左から小さい順にならぶようには見えない。
そこで、深さdepthを辺に持たせた。
insert関数が再帰関数を使うときに深さを増やしていき、辺に深さを登録しておき、すぐには描画しない。
BSTクラスにedges情報をもたせて、辺情報を追加していこう。
edges.append( 深さ、始点、終点、Lかr)
のように。
ついでに、親と同じ数を登録しようとすると、はじかれるようにした。
そして、グラフを描く関数の中で、edgesの1つ1つをすぐに描画しない。
まず、edgesをソートする。前の数値からソートするので、
深さ、始点、終点が小さい順にソートされる。
すると深さの小さい辺、始点が小さい辺、終点が小さい辺
という順になる。
この順にしてから、graphvizに登録すると、同じ深さでは小さい数が左にくる。
以下が改良後のコードだ。
#[IN]Python
#======================
import graphviz
#2分する頂点クラスBT==========================
# dataと左枝と右枝を持つデータ構造(dataは大小判断ができれば何でもよい。)
class BT:
def __init__(self, data):
self.left = None
self.right = None
self.data = data
#2分探索木のクラスBST==========================
# rootから順にBT(data)を入れる。
# rootを含む各点vで、v、v.left、v.rightにBT(data)のデータを入れ続けられます。
class BST:
def __init__(self):
self.root = None
self.edges =[]
# リストから作る。
def make_from(self, lst):
for item in lst:
self.insert(item)
# 1件追加
def insert(self, data):
# vにBTデータをvに入れる。
# vといえば、BTデータとして読んでください。
v = BT(data)
if self.root is None:
self.root = v
else:
self._insert_recursive(self.root, v, 0)
def _insert_recursive(self, v, new_v, depth ):
depth = depth
depth +=1
if new_v.data < v.data:
if v.left is None:
v.left = new_v
self.edges.append([depth,v.data, new_v.data, 'L' ])
else:
self._insert_recursive(v.left, new_v, depth)
elif new_v.data > v.data:
if v.right is None:
v.right = new_v
self.edges.append([depth,v.data, new_v.data, 'r' ])
else:
self._insert_recursive(v.right, new_v, depth)
else:
print(f"データ{v.data}が重複しています。")
# 1件探す
def search(self, data):
return self._search_recursive(self.root, data)
def _search_recursive(self, v, data):
if v is None:
return False
if data == v.data:
return True
elif data < v.data:
return self._search_recursive(v.left, data)
else:
return self._search_recursive(v.right, data)
def show_graph(self):
G = graphviz.Digraph()
lst=sorted(self.edges)
for edge in lst:
depth,source,destination,lbl = edge
G.edge(str(source), str(destination), label = lbl)
return G
# ここからが実行
myBST=BST()
nums = [20,30,40,5,10,15,25,35]
myBST.make_from(nums)
myBST.insert(5)
myBST.insert(50)
myBST.show_graph()
#=====================
[OUT]
データ5が重複しています。
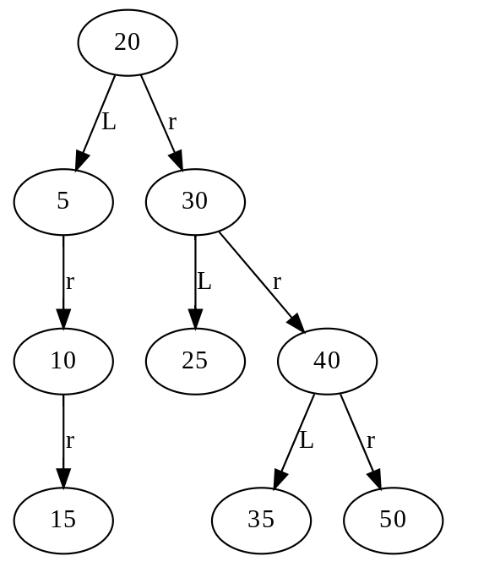
# その他のメソッド (削除、最小値、最大値など)
myBST=BST()
nums = [20,30,40,5,10,15,25,35]
myBST.make_from(nums)
myBST.insert(50)
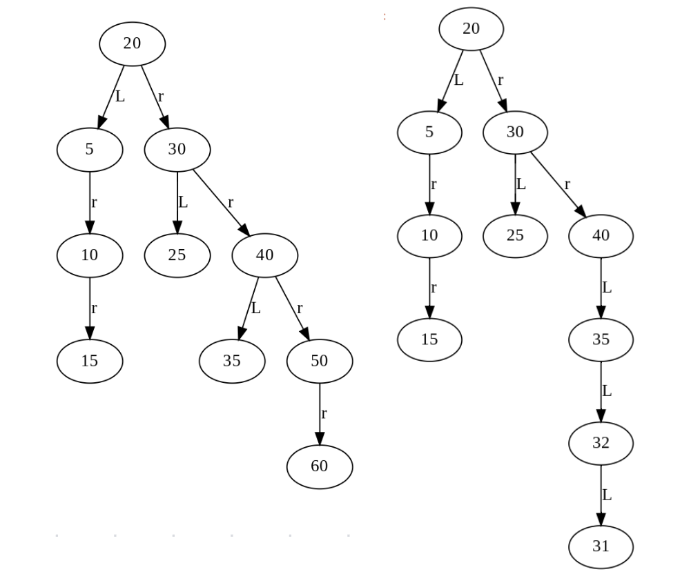
myBST.insert(60)
myBST.show_graph()
のように、どんどん、大きい数を追加すると、木はrの枝が続く。アンバランスだ。
また、
# その他のメソッド (削除、最小値、最大値など)
myBST=BST()
nums = [20,30,40,5,10,15,25,35]
myBST.make_from(nums)
myBST.insert(32)
myBST.insert(31)
myBST.show_graph()
のように、少しずつ小さく数を順に追加すると、木はLの枝が続く。いっそうアンバランスだ。
<データの活用>
BSTを作っているからには、データ追加だけではなく、
最大値、最小値を求めたりもしたいですね。
質問:最大値や最小値を得る関数はどうやれば作れるでしょうか。
BSTを作っているからには、データ追加だけではなく、
最大値、最小値を求めたりもしたいですね。
class BSTのメソッド関数として
次の2つを追加して使えばよいね。
根から左に進み続けて、もう左に行けなくなったときの点の値が最小値
根から右に進み続けて、もう右に行けなくなったときの点の値だ最大値だ。
この考え方をコードにしてみよう。
def min(self):
return self._min_recursive(self.root,None)
def _min_recursive(self, v, previous):
if v.left:
previous = v
return self._min_recursive(v.left, previous)
else:
return v.data
def max(self):
return self._max_recursive(self.root,None)
def _max_recursive(self, v, previous):
if v.right:
previous = v
return self._max_recursive(v.right, previous)
else:
return v.data
# ここからが実行
myBST=BST()
nums = [20,30,40,5,10,15,25,35]
myBST.make_from(nums)
myBST.insert(50)
print(f"min = {myBST.min()}")
print(f"max = {myBST.max()}")
myBST.show_graph()
#=======================
[OUT]
min = 5
max = 50
データの最大、最小を求めるには、別に2分探索木を使わなくても、配列やリストでできます。
データ構造の選択やその実装のコードを改良するということは、
大量のデータを扱う必要がある状況では処理時間を削減することにつながるので、大変価値がある。
あるいは、処理時間を競うコンテストでもそうでしょう。
関心のある人は、さらにコードの改良をめざしてみよう。