Чудові точки трикутника
Чудові точки трикутника
– точки, місце розташування яких однозначно визначається трикутником, не
залежить від його виду та від того, в якому порядку беруться сторони і вершини
трикутника.
Нагадаємо, що пряму, що проходить через середину
відрізка і перпендикулярна до нього, називають серединним перпендикуляром до
відрізка.
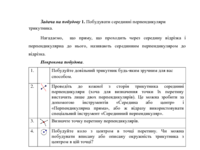
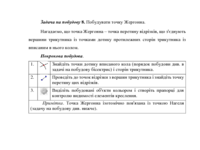
Задача на побудову 1. Побудувати серединні перпендикуляри трикутника.
Навчальне дослідження 1. Дослідіть побудову і
зробіть висновки про властивість точок серединного перпендикуляру щодо їх
відстані до відрізку. Поясніть, чому точка перетину серединних перпендикулярів,
проведених до сторін трикутника, є центром описаного кола трикутника. Це одна з
чудових точок трикутника.
Задача на побудову 2. Створіть прапорець під назвою «Серединний перпендикуляр», який визначатиме видимість побудованих об'єктів (перпендикуляри, чудова точка, коло).
Для зручності сприйняття креслення виділіть побудовані об'єкти іншим кольором.
Задача на побудову 3. Побудувати бісектриси трикутника.
Навчальне дослідження 2. Дослідіть
побудову і зробіть висновки про властивість точок бісектриси кута щодо їх
рівновіддаленості від сторін цього кута. Поясніть, чому точка перетину
бісектрис трикутника є центром вписаного кола трикутника.
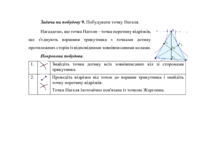
Задача на побудову 4. Побудувати медіани трикутника.
Навчальне дослідження 3. Дослідіть побудову і
зробіть висновки про властивості медіани, а саме:
1) Медіана розбиває трикутник на два трикутники однакової площі.
2)Всі медіани трикутника перетинаються в одній точці, яка ділить кожну з них у відношенні
2:1, рахуючи від вершини. Ця точка називається центром ваги трикутника або його
центроїдом.
Навчальне дослідження 4. Дослідіть побудову і визначте на скільки трикутників розділяється трикутник своїми медіанами. Які трикутники
рівні між собою і чому?
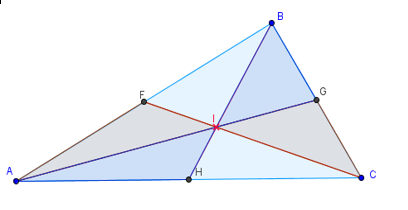
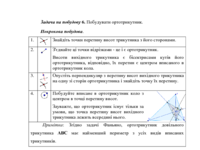
Задача на побудову 5. Побудувати висоти трикутника.
Задача на побудову 6. Побудувати ортотрикутник.
Задача на побудову 7. Побудувати точку Шпікера, зовнівписані кола та точку Бевена.
Задача на побудову 8. Побудувати точку Жергонна.
Задача на побудову 9. Побудувати точку Негеля.
Точки Торрічеллі. Точка Ферма
Точка Торрічеллі – точка трикутника, з якої всі його сторони
видно під кутом в 120°. Існує тільки в трикутниках, кожен з кутів яких менше 120°.
Збігається з точкою Ферма.
Точка Ферма – точка,
сума відстаней від якої до вершин трикутника є мінімальною. Точка Ферма дає
вирішення проблеми Штейнера для вершин трикутника.
Геометрично точка Торрічеллі
– це перетин трьох кіл, які проходять через вершини зовнішніх трикутників.
Зовнішні трикутники – це правильні (рівносторонні) трикутники, побудовані на
сторонах основного трикутника зовнішнім чином.
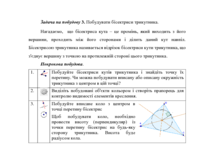
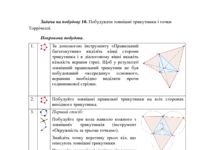
Задача на побудову 10. Побудувати зовнішні трикутники і точки Торрічеллі.
Навчальне дослідження 6. Спробуйте
побудувати другу точку Торрічеллі за цим визначенням. Дослідіть властивості
точки Торрічеллі: сума відстаней від точки до вершин трикутника мінімальна; всі
вершини видно з неї під кутом 120°. Відповідно до визначення точки Торрічеллі,
вона може існувати тільки в трикутнику, всі кути якого менше 120°. Дослідіть
той факт, що якщо у трикутника один кут буде більше 120°, дана точка буде
лежати поза трикутником і втратить свої властивості. При наявності кута,
рівного 120°, точка Торрічеллі збігатиметься з однією із вершин трикутника.
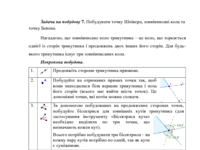
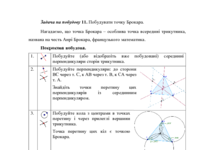
Задача на побудову 11. Побудувати точку Брокара.
Навчальне дослідження 7.
Дослідіть властивості точки Брокара. Які висновки можна зробити про кути, що
формуються відрізком, який з'єднує т. Брокара та прилеглою проти годинникової
стрілки стороною трикутника? (Вони завжди рівні і називаються кутами Брокара.)
З якою точкою у
правильному трикутнику збігається точка Брокара? (з точкою перетину медіан.)
Навчальне дослідження 8. Доведіть, що кут
Брокара ≥ 30°. В яких випадках він буде дорівнювати 30°?
Задача на побудову 12. Побудувати точку Лемуана (Гребе).
Задача на побудову 13. Побудувати точки Аполлонія.
Навчальне дослідження 9. Відобразіть побудовану
раніше точку Лемуана, описане коло, і перевірте, чи дійсно центр описаного кола
і точка Лемуана лежать на осі Брокара.