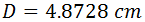Teorema del seno y del coseno
Introducción
Teoremas y Aplicaciones del Seno y Coseno ¡Bienvenidos al emocionante capítulo de los teoremas y aplicaciones del seno y coseno! Aquí, nos sumergiremos en el corazón pulsante de la trigonometría, donde descubriremos cómo estas razones trigonométricas son mucho más que simples funciones: son las claves que abren un universo de posibilidades en la resolución de problemas y en la comprensión del mundo que nos rodea. El seno y el coseno son como dos faros que iluminan nuestro camino a través de las olas de la matemática, guiándonos con su luz constante hacia puertos de conocimiento y comprensión. En este capítulo, no solo aprenderás sobre sus definiciones y propiedades, sino que también explorarás su aplicación en situaciones reales y prácticas. Orientaciones para el Estudio del Seno y Coseno: Con esta introducción, te invitamos a abrir tu mente y a prepararte para una aventura matemática que te llevará desde la teoría hasta la práctica, desde el papel hasta la realidad. ¡Adelante, matemáticos del futuro, el mundo de la trigonometría os espera! A continuación, enunciamos ambos teoremas y daremos un ejemplo de aplicación.
1. Teorema del seno
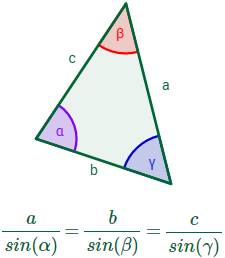
Además, si el triángulo está inscrito en una circunferencia de diámetro D,
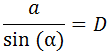
Enlace: Problemas de aplicación del Teorema del seno
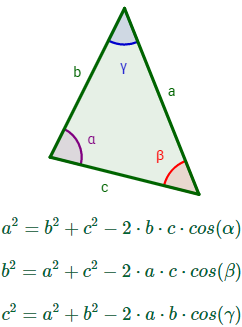
2. Teorema del coseno
Enlace: Problemas de aplicación del Teorema del seno3. Ejemplos de aplicación
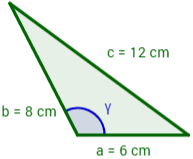Solución:
Aplicamos la siguiente fórmula del teorema del coseno:
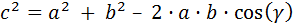
Sólo tenemos que sustituir los datos y aislar el ángulo :
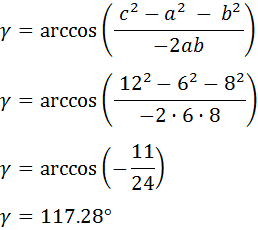
Problema 2
Calcular el radio y el diámetro de la circunferencia en la que está inscrita el siguiente triángulo del que sólo se conoce el ángulo :
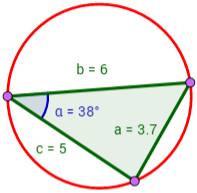Solución:
El teorema del seno proporciona el diámetro D:
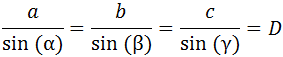
Conociendo ángulo y su lado opuesto, , podemos calcular el diámetro:
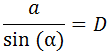
Sustituimos los datos:
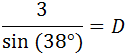
Luego el diámetro mide
