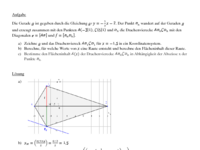
Drachenviereck in Abhängigkeit von x
Beispielaufgabe:
Gegeben ist die Gleichung der Geraden g mit g: y = -0,1x + 3 .
Der Punkt Dn wandert auf der Geraden g und besitzt die Koordinaten Dn(x|-0,1x+3).
Mit den Punkten A(-1|1), Bn , C(7|1) und dem Punkt Dn(x|-0,1x+3) entstehen Drachenvierecke ABnCDn.
a) Zeichne die Punkte A, C und die Gerade g in das Koordinatensystem ein.
b) Zeichne das Drachenviereck AB1CD1 für x = 5 .
c) Berechne den Flächeninhalt A1 des Drachenvierecks AB1CD1 für x = 5.
d) Bestimme den Flächeninhalt A(x) der Drachenvierecke ABnCDn in Abhängigkeit der Abszisse x der
Punkte Dn.
e) Für welche Werte von x entsteht eine Raute?
Lernvideo zur Aufgabe:
Übungsaufgabe
Die Gerade g ist gegeben durch die Gleichung g: y = −x - 2. Der Punkt Bn wandert auf der Geraden g und erzeugt zusammen mit den Punkten A(−3|1), C(6|1) und Dn die Drachenvierecke ABnCDn mit den Diagonalen e = [AC] und f = [BnDn].
a) Zeichne g und das Drachenviereck AB1CD1 für x = −1,5 in ein Koordinatensystem.
b) Berechne, für welche Werte von x eine Raute entsteht und berechne den Flächeninhalt dieser
Raute.
c) Bestimme den Flächeninhalt A(x) der Drachenvierecke ABnCDn in Abhängigkeit der Abszisse x der
Punkte Bn.