Teoremi sulle funzioni continue
Se una funzione è continua, gode di una serie di proprietà che apparentemente sembrano banali e sottintese ma che devono essere dimostrate tramite altrettanti teoremi. In questo paragrafo ci limiteremo ad enunciare tali teoremi, interpretarli e vedere alcuni controesempi per cui, mancando la continuità, le proprietà descritte dai teoremi non sono più garantite.
NOTA: indicheremo in blu le ipotesi dei teoremi, cioè le condizioni necessarie affinché siano verificare le proprietà descritte dalle tesi, che saranno indicate in rosso.
TEOREMA DELLA PERMANENZA DEL SEGNO
ENUNCIAZIONE A PAROLE:
Se una funzione è continua nel punto , esiste un intorno di in cui i risultati della funzione hanno lo stesso segno di .
ENUNCIAZIONE FORMALE SIMBOLICA:
CONSIDERAZIONI E DIMOSTRAZIONE INFORMALE:
Se la funzione è continua in , significa che i suoi risultati calcolati per punti vicino ad sono vicini ad , di conseguenza ci si può aspettare che basta considerare valori sufficientemente prossimi ad per ottenere risultati che hanno lo stesso segno di .
ESEMPI E CONTROESEMPI:
Consideriamo la funzione riportata in figura:
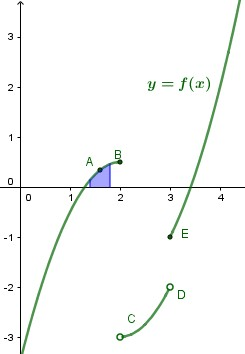
Nel punto A la funzione è continua: riusciamo a trovare un intorno di per cui tutte le al suo interno danno un risultato positivo come . Ad esempio se prendiamo una entro l'intervallo blu, la sua immagine sarà sicuramente positiva.
Nel punto B la funzione presenta una discontinuità di prima specie (del salto) ed infatti la permanenza del segno non vale: non appena consideriamo una appena superiore di , cioè alla sua destra, la corrispondente è negativa e quindi non ha lo stesso segno di .
Da notare che la continuità è condizione sufficiente, ma non necessaria: se c'è la continuità la permanenza del segno è garantita e non c'è bisogno di ulteriori considerazioni; se la funzione non è continua potrebbe comunque esserci la permanenza, solo che non è garantita: per sapere se c'è o no è necessario studiare meglio la funzione. Nel punto E ad esempio la funzione è discontinua, ma la permanenza del segno vale lo stesso.
TEOREMA DEI VALORI INTERMEDI
ENUNCIAZIONE A PAROLE:
Se una funzione è continua in un intervallo chiuso , essa ottiene all'interno dell'intervallo tutti i risultati compresi tra ed .
ENUNCIAZIONE FORMALE SIMBOLICA:
NOTA: per semplicità nel definire l'intervallo abbiamo supposto , ma ovviamente il teorema è simile anche nel caso contrario.
CONSIDERAZIONI E DIMOSTRAZIONE INFORMALE:
Se la funzione è continua in tutti i punti dell'intervallo, significa che mano a mano che mi sposto da in ad i risultati corrispondenti si avvicineranno sempre ai valori effettivamente assunti dalla funzione (continuo a tracciare il grafico senza mai staccare la penna). Se devo arrivare in questo modo da A a B, ne consegue intuitivamente che devo attraversare intero arco di valori che li separa lungo l'asse y. L'unico modo per saltare qualche valore sulle è che la funzione abbia qualche forma di discontinuità in almeno un punto.
TEOREMA DEGLI ZERI
ENUNCIAZIONE A PAROLE:
Se una funzione è continua in un intervallo chiuso e si ha (o viceversa), esiste all'interno dell'intervallo almeno un punto tale che .
ENUNCIAZIONE FORMALE SIMBOLICA:
CONSIDERAZIONI E DIMOSTRAZIONE INFORMALE:
È una diretta conseguenza del teorema dei valori intermedi. Se è positivo e è negativo (o viceversa), esiste nell'intervallo un punto in cui la funzione assume il valore zero, che è uno dei valori intermedi tra un positivo ed un negativo.
TEOREMA DI WEIERSTRASS
ENUNCIAZIONE A PAROLE:
Se una funzione è continua in un intervallo chiuso , la funzione è LIMITATA all'interno dell'intervallo ed ammette sempre un punto di massimo ed un punto di minimo.
NOTA: Una funzione si dice limitata superiormente se esiste un valore , qui chiamato , tale per cui qualunque output sta "sotto" ad , cioè . Analogamente si definisce una funzione limitata inferiormente. Si parla di una funzione che è limitata senza ulteriori specifiche se lo è sia superiormente che inferiormente, quindi se è "confinata" tra un valore minimo ed un valore massimo.
ENUNCIAZIONE FORMALE SIMBOLICA:
Da notare che la seconda tesi (l'esistenza di un punto di minimo e di uno di massimo, è molto più esigente della prima (la limitatezza): la limitatezza afferma semplicemente che i risultati di siano confinati tra due valori; mentre la seconda tesi promette che esisteranno due valori che permettano alla funzione di generare dei risultati che siano rispettivamente il minore ed il maggiore ottenuto dalla funzione. Questi valori estremi non sono più dei numeri qualsiasi ma sono due risultati ottenibili tramite la funzione stessa, e quindi in relazione stretta con essa e le sue caratteristiche.
Capiremo ancora meglio questa differenza nell'animazione qui sotto.
COMBINARE WEIERSTRASS ED I VALORI INTERMEDI
Se combiniamo i due teoremi di Weierstrass e dei valori intermedi, otteniamo che
ENUNCIAZIONE A PAROLE:
Se una funzione è continua in un intervallo chiuso , preso un qualsiasi valore compreso tra l'output minimo e quello massimo generati all'interno nell'intervallo stesso, esiste un nell'intervallo che ha come output proprio quel valore..
In poche parole una funzione continua genera tutti i risultati compresi tra il suo output minimo e quello massimo.
Infatti
1) il teorema di Weierstrass ci garantisce l'esistenza dei punti di minimo e di massimo
2) a questo punto è sufficiente considerare l'intervallo definito dai due valori ed ; esso è contenuto nel precedente, quindi la funzione è continua e posso applicargli il teorema dei valori intermedi.
Lo vediamo nell'animazione qui sotto.