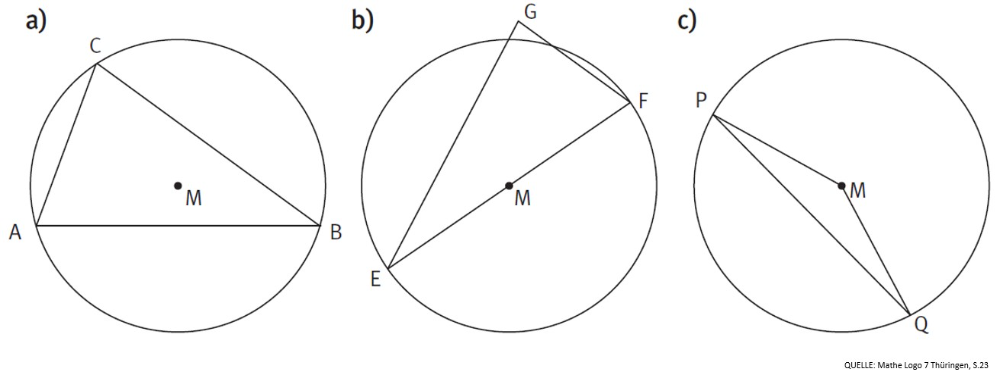
Satz des Thales
Mit einem Geodreieck, zwei Stiften und einem Bleistift einen Kreis zeichnen? Das geht, probiert es aus!

Überprüft eure Beobachtungen aus der ersten Erarbeitung mithilfe der GeoGebra-Anwendung. Verschiebt den Punkt C und beobachtet Veränderungen.
Überprüft eure Schlussfolgerungen mithilfe der nachfolgenden Fragen.
Nenne Beobachtungen.
Hefteraufzeichnungen
Überschrift: 2. Satz des Thales
- Übernimm einen Screenshot der GeoGebra-Anwendung, auf dem sowohl der Winkel im Punkt C als auch der gesamte Halbkreis abgebildet ist.
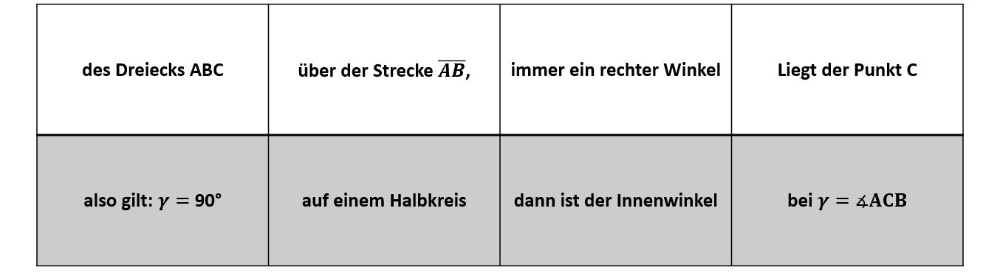
- Formuliere anschließend selbstständig mithilfe der nachfolgenden Vorlage den Satz des Thales.
Übung 1 - Konstruktion
Konstruiere ein rechtwinkliges Dreieck ABC mit c = 5 cm, a = 3 cm und = 90°. Eine Lösung zum Auflegen erhältst du am Lehrertisch.
Übung 2 - Fehlersuche
Übernimm die Abbildung in deine Aufzeichnungen. Beschreibe jeweils, welche Fehler bei der Konstruktion eines rechtwinkligen Dreiecks mit Hilfe vom Satz des Thales entstanden sind.