Додаткові дослідження властивостей трикутника
Пряма Ейлера
У 1765 році німецький
математик Ейлер довів, що в будь-якому трикутнику ортоцентр, центр ваги і центр
описаного кола лежать на одній прямій, яка пізніше була названа прямою Ейлера.
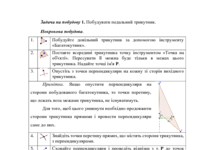
т. J – перетин висот;
т. I – перетин медіан,
центр ваги трикутника;
т. D – перетин
серединних перпендикулярів, центр описаного кола.
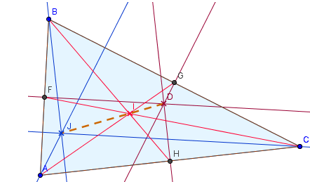
Навчальне дослідження 1.
Побудуйте пряму Ейлера та дістаньтеся висновків, що в прямокутному трикутнику
пряма Ейлера збігається з проведеною до гіпотенузи медіаною; в рівносторонньому
трикутнику пряма Ейлера вироджується в точку.
Коло Ейлера
У двадцятих роках XIX століття французькі
математики Понселе, Бріаншон та інші встановили незалежно один від одного таку
теорему: основи медіан, основи висот і середини відрізків висот, що
з'єднують Ортоцентр з вершинами трикутника, лежать на одному й тому ж колі. Це
ж коло називають колом Ейлера або колом дев'яти точок [7].
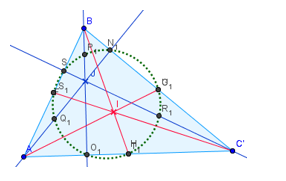
Пряма Сімсона
Для довільного
трикутника основи перпендикулярів, опущених з будь-якої точки описаного навколо
нього кола на його сторони або їх продовження, лежать на одній прямій, яка
називається прямою Сімсона [8].
Задача на побудову 1. Побудувати пряму Сімсона.
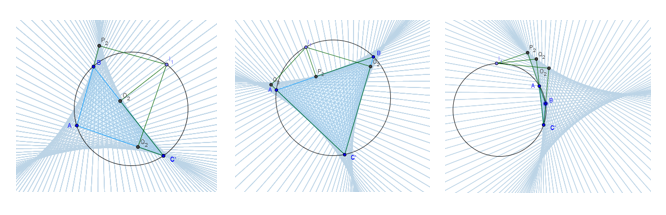
Навчальне дослідження 1.
У властивостях побудованої прямої Сімсона встановіть прапорець «Залишати слід»
і анімуйте точку на колі. Спостерігайте за результатами і переконайтесь, що в
обрисах фігури, сформованої слідом прямої Сімсона в результаті анімації, можна
впізнати гіперболічний трикутник. Незалежно від виду та форми вихідного трикутника,
гіперболічний трикутник завжди буде рівностороннім. Його розмір визначається
радіусом описаного навколо вихідного трикутника
кола. Докладніше про гіперболічний трикутник див. у розділі 8.
Педальний (подерний) трикутник
Трикутник, вершинами
якого є основи перпендикулярів, опущених із точки на прямі, які містять сторони
вихідного трикутника, називається педальним. Точка, з якої опущені
перпендикуляри, також називається педальною [10].