Google Classroom
GeoGebraGeoGebra Classroom
GeoGebra

Potensfunksjoner og rotfunksjoner

Author:Eva Holthe Enoksen
Du skal nå arbeide med og utforske potensfunksjoner og rotfunksjoner. Du lærte om disse funksjonene i 1T, men vi skal nå bygge videre på dette og se hvordan vi kan derivere funksjonene.

Oppgave 1:

Det generelle uttrykket for en potensfunksjon er . Du finner en sånn funksjon i feltet over. Dra i gliderne for å utforske hvilken rolle de to koeffisientene spiller. Legg spesielt merke til hva som skjer i de tre tilfellene under og beskriv dette. - b>0 - 0<b<1 - b>1

Oppgave 2

I hvilke av tilfellene er f en rotfunksjon?

Select all that apply
  • A
  • B
  • C
Check my answer (3)
I 1T lærte du noen regleregler for røtter og potenser som kan komme til nytte nå
I 1T lærte du noen regleregler for røtter og potenser som kan komme til nytte nå

Oppgave 3

Huk av for påstandene som er sanne:

Select all that apply
  • A
  • B
  • C
  • D
Check my answer (3)

Derivasjon av potens- og rotfunksjoner

Vi skal nå derivere potens- og rotfunksjoner. Vi kan bruke derivasjonsformelen vi har lært for polynomer, så lenge vi holder tunga rett i munnen og også husker på potensreglene over. Vi vet at .

Eksempel

Eksempel

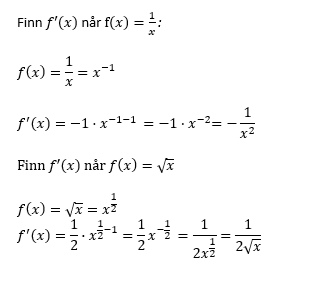
Oppgave 4

Hva blir den deriverte til ?

Select all that apply
  • A
  • B
  • C
  • D
Check my answer (3)

Oppgave 5

I geogebrafeltet over finner du funksjonen , dens deriverte samt en tangent. Du kan selv velge hvilket punkt tangenten skal tangere funksjonen i. Dra i glideren for a og undersøk om sammenhengen mellom stigningstallet til tangenten og funksjonsverdien til den deriverte fremdeles gjelder. Beskriv det du finner i feltet under.

Oppgave 6

Vis ved regning at likningen for tangenten i (1, f(1)) er y = -x+2

Ferdig?

Gjør følgende oppgaver i boka (Står også i OneNote): 8.10, 8.11, 8.111, 8.113, 8.114, 8.301 Det blir en felles gjennomgang av

Select all that apply
  • A
  • B
Check my answer (3)

New Resources

Discover Resources