Google Classroom
GeoGebraGeoGebra Classroom
GeoGebra

2. La cuerda vibrante

Author:Rafael Losada Liste
Esta actividad pertenece al libro de GeoGebra Música y Matemáticas. Dos problemas peliagudos Hasta el siglo XVIII, la matemática no se encuentra lo suficientemente avanzada como para abordar dos problemas intrigantes:
  1. El problema de la cuerda vibrante: Determinar el movimiento de una cuerda tensa al pulsarla.
  2. Demostrar o rebatir la relación de Mersenne: Dada la longitud y el peso de una cuerda, así como la fuerza que la tensa, encontrar el tiempo de vibración.
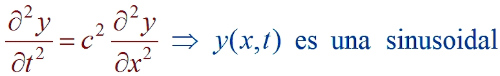Brook Taylor En 1715, Taylor encuentra que el movimiento de un punto arbitrario de la cuerda es el de un péndulo simple y determina su tiempo de vibración (periodo). Obtiene en su lenguaje propio, un tanto distinto del nuestro, la ecuación diferencial de la cuerda vibrante, es decir la ecuación unidimensional de ondas, y a partir de ella halla una solución: la forma de la curva que toma la cuerda en un instante dado es sinusoidal.

Brook Taylor (1685 - 1731)

New Resources

Discover Resources

Discover Topics