3.1/3.2 Integral de línea
Integral de línea
Usualmente se define a la integral como el área bajo la curva, nos da el valor del área de esta misma. Pero si la función que se tratase fuera vectorial ¿se manejaría de la misma manera?. La integral de linea es lo que describe en un caso particular. Se tiene una curva r en R2 que esta parametrizada. Aparte de esto se tiene una superficie en R3. Si imagináramos una especia de cortina entre la curva el techo de la superficie, ¿Cuál seria el área de esta?. Para ello se usaría la integral que lo que hace es sumar infinitas partes sobre una región dada. La región dada seria el intervalo de t (a,b) sobre el cual se quiere obtener el área. Se sumarian infinitos rectángulo, estos rectángulos tendrían como altura la superficie f(x,y) y de base será la el cambio en la curva ds.
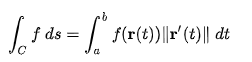
La base se debe poner en términos de t para que se pueda integrar. Entonces para ello ds seria igual al vector tangente ya que este es un cambio sobre la dirección del punto evaluado y se le sacaría el modulo para tener la medida de la base, de esta manera se tendría la forma de sacar integrales de linea.