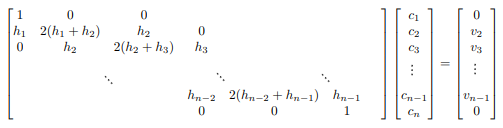Propiedades de la spline cúbica
Spline cúbica
Dada una serie de puntos donde las abcisas no son necesariamente equidistantes pero si convenientemente ordenadas de forma que <...<, diremos entonces que una función spline de grado o spline cúbica, es una función definida en el intervalo compuesta por un conjunto de polinomios o trazadores cúbicos de la forma para cada
que satisfacen las siguientes condiciones: a) para cada ; b) para cada c) para cada d) para cada e) Se cumple una de las siguientes condiciones de frontera- (frontera libre o frontera natural, spline cúbica natural)
- y , (spline cúbica fija con frontera sujeta)
La ecuación a) indica que la spline cúbica se ajusta a cada uno de los puntos, b) que es continua, c) y d) que es continua en pendiente y curvatura a lo largo de toda la región generada por los puntos. Observe que dados puntos a interpolar, se necesitarán trazadores cúbicos lo cual implica que tendremos como incógnitas a y para . A continuación veremos la forma de construir éstos trazadores y como hallar cada una de las incognitas.
Construcción de trazadores cúbicos
Para construir el spline cúbico , se pueden aplicar las condiciones anteriores a los trazadores cúbicos. Observe que si entonces y si se aplica la condición b), para cada . Introducimos la notación para cada si además definimos , se puede ver que ésto implica que la ecuación para cada . De manera similar definimos y observamos para : para cada , aplicando la condición c), para cada . Otra relación entre los coeficientes se obtiene para : para cada , aplicando la condición d) y definiendo para cada Despejando de la ecuación anterior y sustituyendo para cada y luego una reducción del indice de despejamos , con una reducción del indice reemplazando y en , tenemos
operando algebraicamente, nos queda introduciendo la notación para cada . Este sistema tiene como incógnitas sólo a ya que los valores y están dados por el espaciamiento entre las abcisas y sus respectivos valores deNótese que una vez que se conocen los valores de , encontrar los valores de las constantes de la ecuación , de la ecuación y construir los trazadores cúbicos resulta una cuestión sencilla. Si se cumplen las condiciones de frontera libre implican que
De acuerdo con Zapata (s.f) las dos ecuaciones y junto con las ecuaciones en producen un sistema lineal descrito por la ecuación vectorial , lo que nos da un total de ecuaciones con incognitas lo cual puede escribirse en la forma matricial