toonladders
Als je iemand vraagt: "Wat is een toonladder?" is de kans dat je het volgende krijgt:
De zogenaamde grote tertstoonladder is een opeenvolging van 7 stamtonen do-re-mi-fa-sol-la-si.
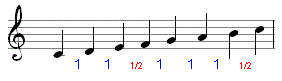Deze opeenvolging komt op een piano overeen met de naast elkaar liggende witte toetsen.
Merkwaardig is dat de afstanden tussen de verschillende tonen niet even groot is.
De afstand tussen de 1e toon (do) en de 2e (re) is een hele toon.
De afstand tussen de 3e toon (mi) en de 4e (fa) is maar een halve toon.
Dit lijkt heel onlogisch. Waarom twee keer een halve toonafstand nemen?
Als je die twee halve toonafstanden zou samenvoegen zouden alle toontrappen toch even groot zijn...
Het laatste waarvan je Pythagoras zou verdenken is niet logisch te denken.
Pythagoras onderzoekt welke samenklinkende tonen als welluidend worden ervaren.
Deze samenklanken gebruikt hij om de toontrappen binnen een octaaf te bepalen, maar daar komen we verder nog op terug.
Toch kunnen we ook in stapjes van halve tonen van do naar do:
Deze opeenvolging komt op een piano overeen met de naast elkaar liggende witte toetsen.
Merkwaardig is dat de afstanden tussen de verschillende tonen niet even groot is.
De afstand tussen de 1e toon (do) en de 2e (re) is een hele toon.
De afstand tussen de 3e toon (mi) en de 4e (fa) is maar een halve toon.
Dit lijkt heel onlogisch. Waarom twee keer een halve toonafstand nemen?
Als je die twee halve toonafstanden zou samenvoegen zouden alle toontrappen toch even groot zijn...
Het laatste waarvan je Pythagoras zou verdenken is niet logisch te denken.
Pythagoras onderzoekt welke samenklinkende tonen als welluidend worden ervaren.
Deze samenklanken gebruikt hij om de toontrappen binnen een octaaf te bepalen, maar daar komen we verder nog op terug.
Toch kunnen we ook in stapjes van halve tonen van do naar do:In dezelfde opeenvolging van hele en halve tonen kunnen we ook starten vanuit andere tonen dan een do.
Hierbij kan je de kwintencirkel volgen:
 | Twee toonsoorten die een kwint uit elkaar liggen hebben 6 van de 7 tonen gemeen. Volg je de kwintencirkel in wijzerzin, dan verschijnt er in de voortekening aan de sleutel telkens 1 kruis extra. Volg je de kwintencirkel tegenwijzerzin dan verschijnt er in de voortekening aan de sleutel telkens 1 mol extra. We vertrekken hierbij van de toonladder in do groot (C): do - re - mi - fa - sol - la - si - do. Vanaf C één stap in wijzerzin komen we uit op sol groot (G) met 1 verhoogde toon: fa#. sol - la - si - do - re - mi - fa# - sol. Vanaf C één stap in tegenwijzerzin komen we uit op fa groot (F) met 1 verlaagde toon: sib. fa - sol - la - sib - do - re - mi - fa. In de kleine tertstoonladders krijg je eenzelfde verhaal, startend met de toonladder van la klein (a). |
Reeds in de Griekse Oudheid bepaalde men de frequenties van deze stappen vanuit verhouding met
de frequentie van de grondtoon. Toonafstanden met deze verhoudingen noemt men ‘rein’.
| beginnend met do als grondtoon: | do | re | mi | fa | sol | la | si | do |
| rangorde | prime | seconde | terts | kwart | kwint | sext | septime | octaaf |
| frequentieverhouding met de prime is | 1/1 | 9/8 | 5/4 | 4/3 | 3/2 | 5/3 | 15/8 | 2/1 |