ReducedRowEchelonForm - Zeilenstufenform
P {1, 2, 1, -3} == 1. Schritt: Zeile2 += Zeile1*(-3) ← P( lese von rechts nach links) : RRef nur Zeilenoperationen
Notation zur Erzeugung von Elementarmatrizen
Für eine neue Aufgabe zuerst die Matrixlisten zurücksetzen [θ]
Zeilenoperationen
{index, a, b, wert}
[ Pi ] schreibe eine Elementarmatrix Pindex = (ea,b)=wert nach Pindex
Zeilea += Zeileb*wert
[] schreibe eine Elementarmatrix für Element→0 entsprechend der Auswahl der Listboxen in die Inputbox
( Zeile Klick um die Argumente #p in die Inputbox zu kopieren)
[] Checkbox zur Anzeige/Edit(Rundungsfehler ausbessern) Elementarmatrix P#p
[ θ ] initialisiere P mit Einheitsmatrizen
{index, a, b}
[ Pi ] schreibe eine Elementarmatrix/Zeilentausch Pindex = (zeile a b, aindex
{2,3,2,-2} , P2 A --> Zeile3 += Zeile2 * (-2)
Spaltenoperationen (not tested)
{index, a, b, wert}
[ Qi ] schreibe eine Elementarmatrix Qindex= (ea,b)=wert nach Qindex
Spaltea += wert*Spalteb
{index, a, b}
[ Qi ] schreibe eine Elementarmatrix/Spaltentausch Qindex = (spalte a b, aindex
IP = P1...Pp
IQ = Q1 ... Qq
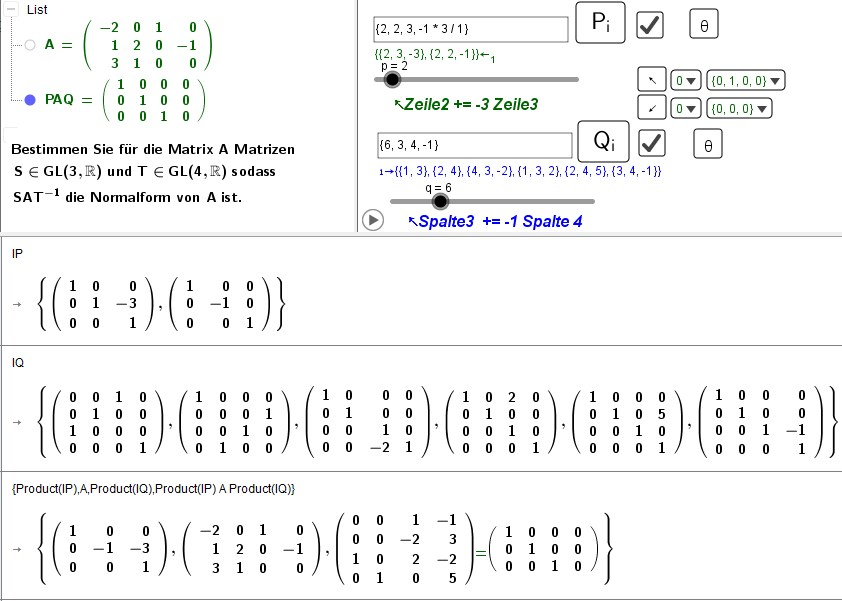
PAQ = Product(IP) A Product(IQ)
Probe
Transpose(Take(Transpose(A),1,n)) Transpose(Take(Transpose(ReducedRowEchelonForm(A)),n+1))
---
Alle Versuche eine steuerbare Entwicklung der Elementarmatrizen im CAS (und damit exakt) darzustellen sind im Zuge der "Weiterentwicklung - updates" zunichte gemacht worden - laufen nur in der 5.x Version lokal und laden in der 6.x (oder Online) nicht mehr. Diese Version hält die Matrizen in der AlgebraView und produziert ggf. Rundungsfehler (auch in der Symbolic-Einstellung) - um einigermaßen "saubere" Darstellungen zu erhalten sollte man Divisionen mit gerundeten Werten (z.B. 1/3 uä.) vermeiden. Evtl. hilft es einen Bruch direkt in eine der Elementarmatrizen P1...P25 zu schreiben..
1. Anwendungsbeispiel: RRef Example Ax = b ==> (Ab) ==> P(Ab) = RRef
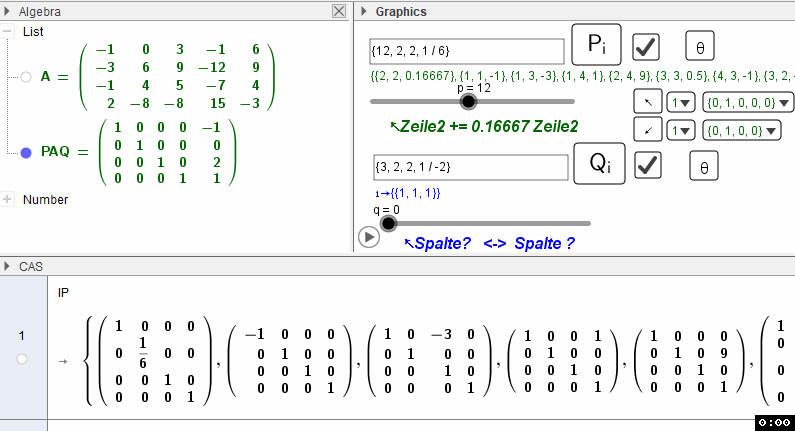
2. Inverse P A = id ==> Product(IP)=A^-1

3. Schnittgerade zweier Ebenen E1, E2

4. Normalform S A T^-1