A - Ein Bild sagt mehr

Zusammenhang im Graph

So richtig vorstellen, wie die Messwerte zusammenhängen, können Sarah und Max es sich immer noch nicht. Max' Mama sagt: "Abbildungen sind immer sehr hilfreich." "Graph" nennt man die Punkte bzw. die Verbindungslinie im Koordinatensystem. Damit kann man einen Zusammenhang mathematisch als Bild darstellen. Setzt nun in der Simulation Kreise-K das Häkchen bei „Messpunkte“. Jetzt erscheinen eure Messwerte aus der Animation im linken Bereich als Messpunkte (Durchmesser, Umfang) im Koordinatensystem rechts.

Kreise-K

Das sieht ja schon mal irgendwie regelmäßig aus, aber was erkennt man dabei... Beschreibt eure Beobachtung.

Max und Sarah haben sich überlegt, dass es helfen könnte die Punkte miteinander zu verbinden. Aber sie sind unsicher: darf man das denn einfach so machen? Hier seht ihr einen vergrößerten Ausschnitt des Graphen:

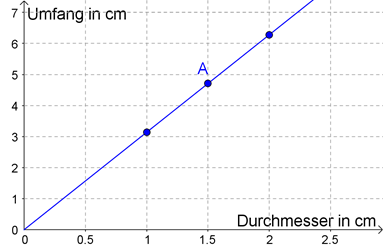
Welche Informationen könnt ihr dem Punkt A über den dazugehörigen Kreis entnehmen?

Sind diese Information, die in Punkt A stecken, inhaltlich sinnvoll? Begründet!

Kommen wir wieder zu der Frage von Max und Sarah zurück: Darf man die Punkte hier verbinden? Begründet!

So geschafft. Jetzt passt alles. Setzt in der Simulation Kreise-K ein Häkchen bei "Trendlinie", damit werden die Punkte verbunden. Der Graph beschäftigt Sarah und Max aber immer noch… Was ist denn jetzt mit dem Zusammenhang...

So ein Graph lässt sich auch gut mit Worten beschreiben. Begründet kurz, warum diese drei Wörter gut zu euren Graphen passen: a) steigen b) gleichmäßig c) gerade

Verbindet jetzt die Eigenschaften des Graphen aus der vorherigen Aufgabe mit dem von Sarah und euch formulierten Satz zum Zusammenhang zwischen Durchmesser und Umfang des Kreises aus Aufgabe 8 (Abschnitt "Das geht genauer -K"). Fasst beides in einem Satz zusammen.

Gut gemacht! Jetzt könnt ihr für Sarah und Max die benötigte Länge des Seils ausrechnen: Um den Stamm (Durchmesser 40 cm) müssen sie dreimal rum mit dem Seil. Zwei Äste sollen doppelt umwickelt werden (Durchmesser 18 und 21 cm). Und bei einem weiteren Ast (Durchmesser 16 cm) wird das Seil nur einfach drum gebunden. Für jedes Mal Binden rechnen sie noch 40 cm Seil zum verknoten ein. Wie viele Meter Seil müssen die beiden besorgen? Notiert eure Rechnung und die Antwort.

SO!!! Fertig mit den Baumscheiben. Nur kurz ein bisschen aufräumen und weiter geht's: Packt die Holzscheiben wieder zurück in die Materialbox.

A - Ein Bild sagt mehr

Zusammenhang im Graph

Kreise-K

Nuevos recursos

Descubrir recursos

Descubre temas