Aplicación del Método de Bisección
¿Cómo empleamos el método de Bisección?
El método consiste en dividir por la mitad repetidamente los subintervalos de d y en cada paso localizar la mitad que contiene la solución de .
Para visualizar cada iteración es necesario realizar una tabla la cual contendrá los valores correspondientes a cada aproximación del polinomio.
Tomemos como referencia la siguiente función:
La tabla contendrá 7 columnas de la siguiente manera:
Donde:
Para la sucesión de tenemos:
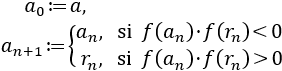 Para la sucesión de tenemos:
Para la sucesión de tenemos:
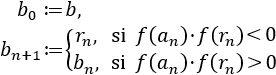 En la siguiente escena tenemos la tabla y la interpretación gráfica de la función; en esta escena podrás ingresar la función así como los valores de y
En la siguiente escena tenemos la tabla y la interpretación gráfica de la función; en esta escena podrás ingresar la función así como los valores de y
| | | | | | | | |
| 1 | 1.5 | 1.25 | -5 | 2.375 | -1.796875 | 0.25 | 1 |
| 1.25 | 1.5 | 1.375 | -1.796875 | 2.375 | 0.16210938 | 0.125 | 2 |
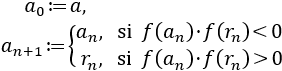 Para la sucesión de tenemos:
Para la sucesión de tenemos:
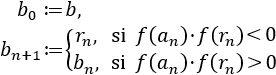 En la siguiente escena tenemos la tabla y la interpretación gráfica de la función; en esta escena podrás ingresar la función así como los valores de y
En la siguiente escena tenemos la tabla y la interpretación gráfica de la función; en esta escena podrás ingresar la función así como los valores de y
¿Cómo interpretamos el ejemplo anterior?
- El deslizador mostrado en la escena (n) representa el número de iteración del método de bisección.
- La tabla representa la aplicación del método pasó por paso.
- En la interpretación gráfica se muestran 3 puntos, cuando estos puntos se unen, significa que converge y encontramos el punto de solución. En este caso en la iteración número 7.