Симетрале сва три угла троугла секу се у једној тачки
Доказ:
Нека је произвољан троугао и нека су f и g симетрале углова код темена B и C троугла. Ако је њихов пресек тачка D и тачке F, E, G подножја нормале из D на странице троугла AB, BC, AC.
Из D припада f следи , а из D припада g следи .
Значи , а одатле следи D припада симетрали угла код темена A.
Доказ:
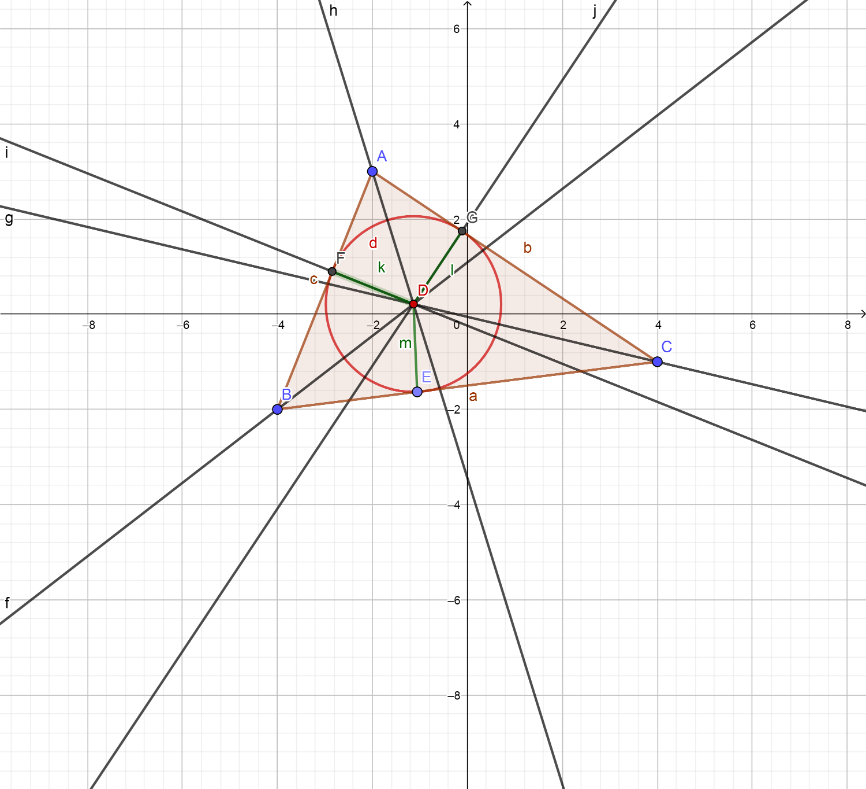
Тачка у којој се секу симетрале унутрашњих углова троугла назива се центар уписане кружнице троугла.
Полупречник тог круга је растојање центра до било које странице троугла.
У сваки троугао може се уписати круг.