Triángulos (Evaluación de los aprendizajes)
Elementos, clasificación y propiedades:
1) Utiliza los deslizadores para modificar los valores de los lados a, b y c del triángulo. Observa los cambios.
a) Copia en tu carpeta y completa la tabla con SI o NO, justificando tu respuesta:
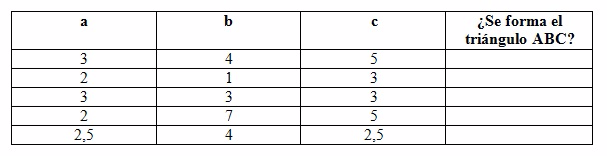
b) ¿Puedes estar seguro, sin hacer el dibujo, de si se pude o no construir un triángulo cuyos lados midan 8 cm, 5 cm y 3 cm? Justifica tu respuesta.
Conclusión:
La suma de las longitudes de dos lados cualesquiera de un triángulo es _ _ _ _ _ _ _ _ _ que el tercer lado.
2) Utiliza los deslizadores para modificar los valores de los ángulos interiores α y β del triángulo ABC y observa los cambios.
a) Copia en tu carpeta y completa la tabla, justificando tu respuesta:
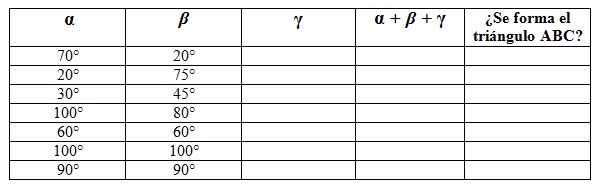
b) ¿Puedes estar seguro, sin hacer el dibujo, de si se pude o no construir un triángulo cuyos ángulos interiores midan 80°, 20° y 90° respectivamente? ¿Por qué?
c) Un triángulo tiene un ángulo interior de 55°, otro de 35° y el tercero de 90°. ¿Cuántos triángulos distintos que cumplan esta condición pueden construirse?
Conclusión:
En todo triángulo, la suma de los ángulos interiores es igual a _ _ _ _ _ _ _ _ _
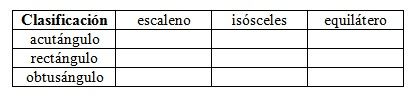
3) Mueve los vértices del triángulo ABC para que satisfaga las dos condiciones (cuando sea posible). Copia en tu carpeta y completa la tabla con SI o NO. Justifica tu respuesta.
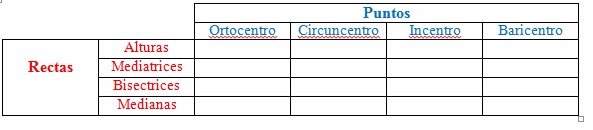
Puntos notables del triángulo:
Construye un triángulo cualquiera ABC en la siguiente hoja de trabajo de GeoGebra:
-Marca los puntos A, B y C, con la herramienta “punto”.
-Construye el triángulo uniendo los puntos A, B y C, con la herramienta “polígono”.
4) a) Traza las alturas (rectas que pasan por uno de sus vértices y son perpendiculares al lado opuesto
de dicho vértice) correspondientes a cada uno de sus lados del triángulo ABC, para lo cual debes utilizar la herramienta “perpendicular” de cada lado, que pase por el vértice opuesto.
b) ¿Las alturas se cortan en algún punto? (usa la herramienta “intersección”).
Mueve los vértices ABC para obtener diferentes triángulos y analizar tu respuesta.

5) a) Traza las tres mediatrices (rectas que pasan por el punto medio de cada uno de sus lados y son perpendiculares a los mismos) del triángulo ABC. Utiliza la herramienta “mediatriz”.
b) ¿Las tres mediatrices se cortan en algún punto? (usa la herramienta “intersección”).
Mueve los vértices ABC para obtener diferentes triángulos y analizar tu respuesta.
c) Dibuja la circunferencia con centro en ese punto de intersección y que pasa por uno de los vértices. ¿Pasará por los tres vértices simultáneamente? Utiliza el botón “circunferencia (centro, punto)”.

6) a) Traza la bisectriz (lugar geométrico de los puntos del plano que equidistan de los dos lados del ángulo) de cada ángulo del triángulo ABC. Utiliza la herramienta “bisectriz” en sentido de las agujas del reloj.
b) ¿Las tres bisectrices se cortan en el mismo punto? (usa la herramienta “intersección”).
Mueve los vértices ABC para obtener diferentes triángulos y analizar tu respuesta.
c) Dibuja la circunferencia con centro en ese punto de intersección y que sea tangente a uno de los lados del triángulo. ¿Será tangente a los tres lados simultáneamente?
Para analizar esta cuestión debemos realizar los siguientes pasos en GeoGebra:
-Traza la recta perpendicular a uno de los lados que pasa por el punto de intersección de las
bisectrices, utilizando la herramienta “perpendicular”.
- Busca el punto de intersección entre la recta anterior y dicho lado, para lo cual debes usar la herramienta “intersección”.
- Construye la circunferencia con centro en el punto de intersección de las bisectrices que pase por el punto de intersección anteriormente hallado. Utiliza el botón “circunferencia (centro, punto)”.

7) a) Traza las medianas (segmentos que unen el punto medio de un lado del triángulo con el vértice opuesto) correspondientes al triángulo ABC, para lo cual debes utilizar la herramienta “medio o centro” de cada lado, y traza los segmentos que pasen por ese punto medio y el vértice opuesto al lado (botón
“segmento”).
b) ¿Las medianas se cortan en algún punto? (usa la herramienta “intersección”).
Mueve los vértices ABC para obtener diferentes triángulos y analizar tu respuesta.

c) “La parte de la mediana que está comprendida entre el baricentro y el lado correspondiente a ella equivale a un tercio de la longitud total de le mediana”.
Comprueba esta propiedad, midiendo los segmentos determinados (usa la herramienta “distancia o longitud”).
8) Mueve los vértices del triángulo ABC para que satisfaga las condiciones:
a) Copia la tabla en tu carpeta y complétala con INTERIOR, EXTERIOR o SOBRE el triángulo. Justifica tu respuesta

b) Observa los cambios y responde:
¿Podrán ser el incentro y/o el baricentro un punto exterior del triángulo?
9) Observa las rectas rojas y el punto azul de cada triángulo. Copia en tu carpeta y completa la tabla con el número de triángulo que satisfaga ambas condiciones, explicando cada una de tus elecciones