Marinovo válcové zobrazení - class
Marinovo zobrazení je příkladem projekce ekvidistatní v polednících, tj. mp = 1 na celé mapě.
Válcová plocha se dotýká referenční sféry podél rovníku. Sféru zobrazíme na válec tak, aby se zachovaly délky na polednících. Všechny rovnoběžky až na rovník se natahují, největší zkreslení je na pólu.
Předpokládejme, že zeměpisná šířka i délka jsou zadány v radiánech. Potom délka na poledníku, přislušející rozdílu zem. šířky ΔΦ je dána součinem R.ΔΦ.
Při rozvinutí válcové plochy do roviny se zachovají délky na rovníku. Dva body na rovníku s rozdílem zem. délek Δλ se zobrazí do vodorovné úsečky délky R.Δλ.
Zvolíme-li mapu tak, že obraz rovníku je na ose x a obraz nultého poledníku na ose y, jsou zobrazovací rovnice tvaru:
x = R . λ y = R . Φ
Úkoly: Na mapě je zvoleno měřítko tak, aby R = 1.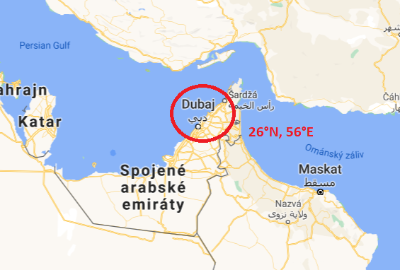
Obraz bodu
Jaké město má na mapě souřadnice (0.54, 0.52)?