Comenzando de cero
Una alternativa, al momento de diseñar una actividad de clase con GeoGebra, es darle al alumno una serie de instrucciones para que haga una construcción en el programa, y luego proponerle algunas preguntas que lo hagan reflexionar acerca de lo que ha hecho, manipulando la construcción. GeoGebra tiene la ventaja de ofrecer, en forma simultánea, varias representaciones de cada objeto matemático. Por ejemplo, se puede trabajar indistintamente con una recta que se define (por ejemplo) a partir de dos de sus puntos, o también con su ecuación. Por esta razón, poner al alumno en situación de interacción con el programa hace que considere familiar este tipo de representaciones simultáneas, profundizando en el sentido de los objetos matemáticos. Cuando proponemos una tarea centrada en un instructivo de construcción es fundamental acompañarla de una buena batería de preguntas que inciten a la reflexión, personal o de pequeños grupos, y donde sea conveniente explorar en las opciones del mismo programa para obtener una respuesta. Veremos que esta metodología es adecuada para explorar propiedades sencillas, que puedan motivar a los alumnos para que ellos mismos redacten un enunciado general. En los ejemplos que trataremos podremos ver estas dos componentes: las instrucciones de uso del software, y la guía para atender a las propiedades relevantes.
Algunos números no cambian
- Ejes: NO
- Cuadrícula: NO
- Atracción de punto a cuadrícula: NO
- Ventana algebraica: VISIBLE
Clic en tres puntos de la zona gráfica (se habrán creado los puntos A, B y C)
Ingresa los siguientes comandos en la línea de entrada (presionando ENTER al final de cada línea), observando especialmente sus efectos:
Recta[A,B]
Recta[A,C]
Punto[a]
Recta[B,C]
Traslada[c,Vector[B,D]]
Interseca[c',b]
Segmento[A,D]
Segmento[A,E]
Segmento[D,B]
Segmento[E,C]
d/e
f/g
Preguntas para los alumnos:
Observa en la ventana algebraica los valor de i y de h. Coloca el puntero del ratón sobre uno de ellos y espera un instante: verás cómo fue definido ese número.
¿Qué particularidad tienen esos números?
Presiona ESC, y luego mueve el punto D. ¿Qué regularidades observas?
Prueba moviendo los puntos iniciales (A, B y C). ¿Qué sucede ahora?
Escribe con tus palabras qué has observado, e intenta redactar una ley que describa la propiedad que parece cumplirse siempre.
Ejercicio
Realiza una propuesta de trabajo similar a la anterior, que permita a los alumnos intuir la relación que hay entre las medidas de los segmentos en que el baricentro de un triángulo divide a una mediana.
(OTRO ejemplo de construcción guiada por el profesor: Relaciones ocultas
- Ejes: SÍ
- Cuadrícula: NO
- Atracción de punto a cuadrícula: Automático
- Ventana algebraica: VISIBLE
Clic en dos puntos de la zona gráfica.
Observa la ecuación de la circunferencia c en la zona algebraica, y observa las coordenadas de su centro.
¿Qué relación detectas entre ellos? Mueve los puntos A y B para corroborar tus conjeturas.
Ahora cambiaremos la presentación de la ecuación. Clic derecho sobre la ecuación de c o sobre la circunferencia, y luego seleccionar la otra modalidad para visualizar la ecuación: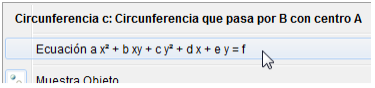
Ejercicio
Realiza una propuesta de trabajo similar a la anterior, que permita a los alumnos descubrir la relación que hay entre las ecuaciones de dos rectas paralelas.