Función racional: hipérbola
Fun ción exponencial: tipo de gráfica
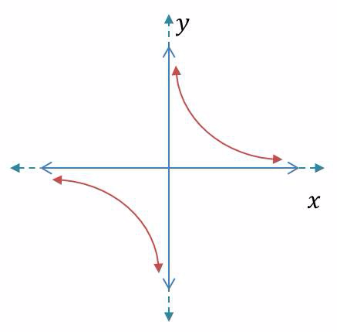
Explicación de la función racional
Propiedades de las funciones racionales:
-El dominio está formado por los valores de R excepto los que anulan el denominador.
-Para cada valor de x que anula el denominador tenemos una asíntota vertical: Q(a)=0 x=a es una asíntota vertical de f(x).
-Si x=a es una raíz simple de Q(x)=0, las ramas laterales de la asíntota x=a tiene sentido distinto, una hacia y la otra a . Si x=a es una raíz doble, ambas ramas van hacia + o hacia -.
-Si el grado de P(x) es una unidad mayor que el grado de Q(x) existe una asíntota oblicua, la misma, tanto si x como si x .
-Si P(x) y Q(x) tienen el mismo grado, hay una asíntota horizontal en y=m/n siendo m y n los coeficientes respectivos de mayor grado de P(x) y Q(x).
-Si el grado de P(x) es menor que el de Q(x) hay una asíntota horizontal en y=0.
Podemos encontrar puntos de inflexión y puntos singulares.