de normale verdeling
Histogrammen vertonen vaak een symmetrische, klokvormige verdeling,
die we goed kunnen benaderen door een vloeiende kromme. We noemen ze dichtheidskrommen.
Vaak stellen we bij deze krommen vast:
Zulke krommen noemen we normale krommen.
Carl Friedrich Gauss onderzocht het verloop. We noemen ze daarom ook Gausscurve.
Hij vond ook het voorschrift:
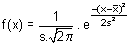We noteren deze verdeling als Norm (μ,σ) met:
μ als het gemiddelde van de verdeling
σ (= s) als standaardafwijking
| - ze zijn symmetrisch ten opzichte van een verticale door het gemiddelde - de meeste waarden liggen in de buurt van het gemiddelde - hoe verder weg van het gemiddelde, hoe minder waarden |
We noteren deze verdeling als Norm (μ,σ) met:
μ als het gemiddelde van de verdeling
σ (= s) als standaardafwijking Verken de invloed van gemiddelde en standaardafwijking op de dichtheidskromme
Hoe verandert de kromme als je het gemiddelde verhoogt?
Hoe verandert de kromme als je de standaardafwijking verhoogt?