2.5 Funciones trascendentes: trigonométricas, logarítmicas y exponenciales.
Funciones trigonométricas
Toda función trigonométrica es periódica es decir que tiene un ciclo o periodo que se repite indefinidamente. Ejemplo: los días de la semana, empezando por lunes termina en domingo, y se inicia nuevamente el periodo de 7 días. Las razones trigonométricas son utilizadas para encontrar el lado o Angulo en un triángulo rectángulo. Las funciones trigonométricas son las relaciones entre los lados de un triángulo.
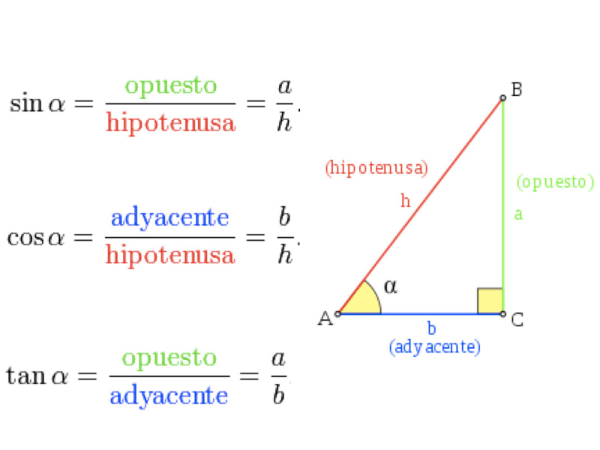
Razones trigonométricas
Para representar las funciones trigonométricas de manera gráfica se puede realizar una tabulación y graficar el resultado, o se aplica el método de proyección. Ejemplo sen x.
Si existe una constante dentro de la función seno, afectará la frecuencia de la misma; si es mayor que un entero aumentará la frecuencia de la función, y si es menor la disminuirá. Por otra parte, si la constante se encuentra afuera de la función afectará el rango de la misma, aumentándolo si es mayor que 1 y disminuyéndola si es menor que 1. Esto también es válido para la función cos(x).
La gráfica de la función coseno siempre toca el punto (0,1) si es positiva, pero si es negativa su gráfica está en espejo con respecto al eje x y tocará el punto (0,-1). Su dominio es (-∞,∞) y su imagen está dada por [ -1,1]. Igual que en la función seno, su frecuencia y su amplitud se modifican si existen constantes dentro o fuera de la función, respectivamente
La gráfica de la función cotangente es espejo de la función tangente. La función cotangente no toca el origen. Si afectamos el interior o el exterior de la función, obtendremos el mismo resultado que en la función tangente al modificar la frecuencia o amplitud de la misma. El dominio y rango de la función están dados por
y (-∞,∞).
Funciones exponenciales.
Este tipo de funciones son particularmente importantes en la vida diaria pues ayuda a representar el incremento poblacional de los seres vivos. Una función exponencial se define de manera general como: f(x)=ax, donde a es la base de la función y es una constante positiva. Las funciones exponenciales más utilizadas son: f(x)=10x función exponencial de base 10 f(x)=ex función exponencial de base e Conceptos importantes sobre la función exponencial 1. La gráfica de toda función exponencial pasa por el punto (0,1). 2. El dominio son todos lo números reales (-∞,∞). 3. El rango son todos los números reales positivos (0,∞).
Funciones logarítmicas
- La gráfica de toda función logarítmica pasa por el punto (1,0).
- El dominio son todos los números reales positivos (0,∞).
- El rango son todos los números reales (-∞,∞).