1. Methode
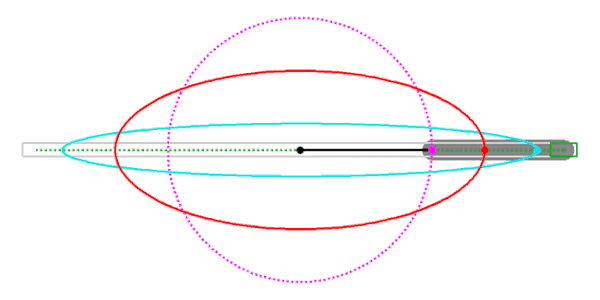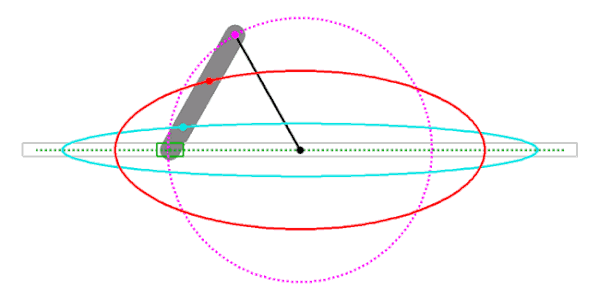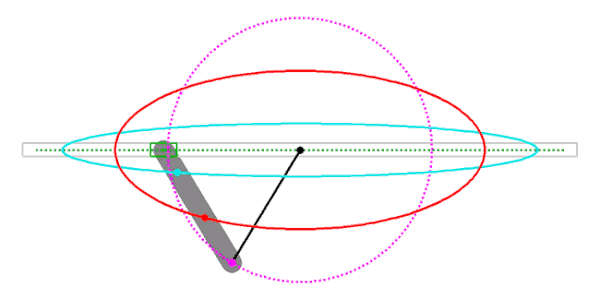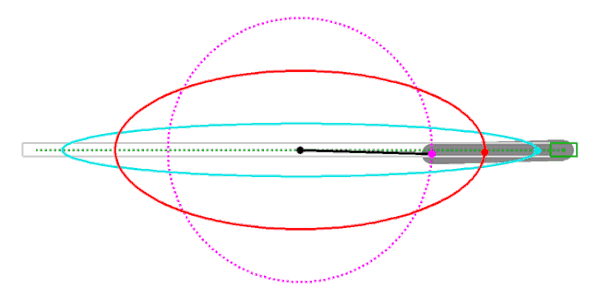
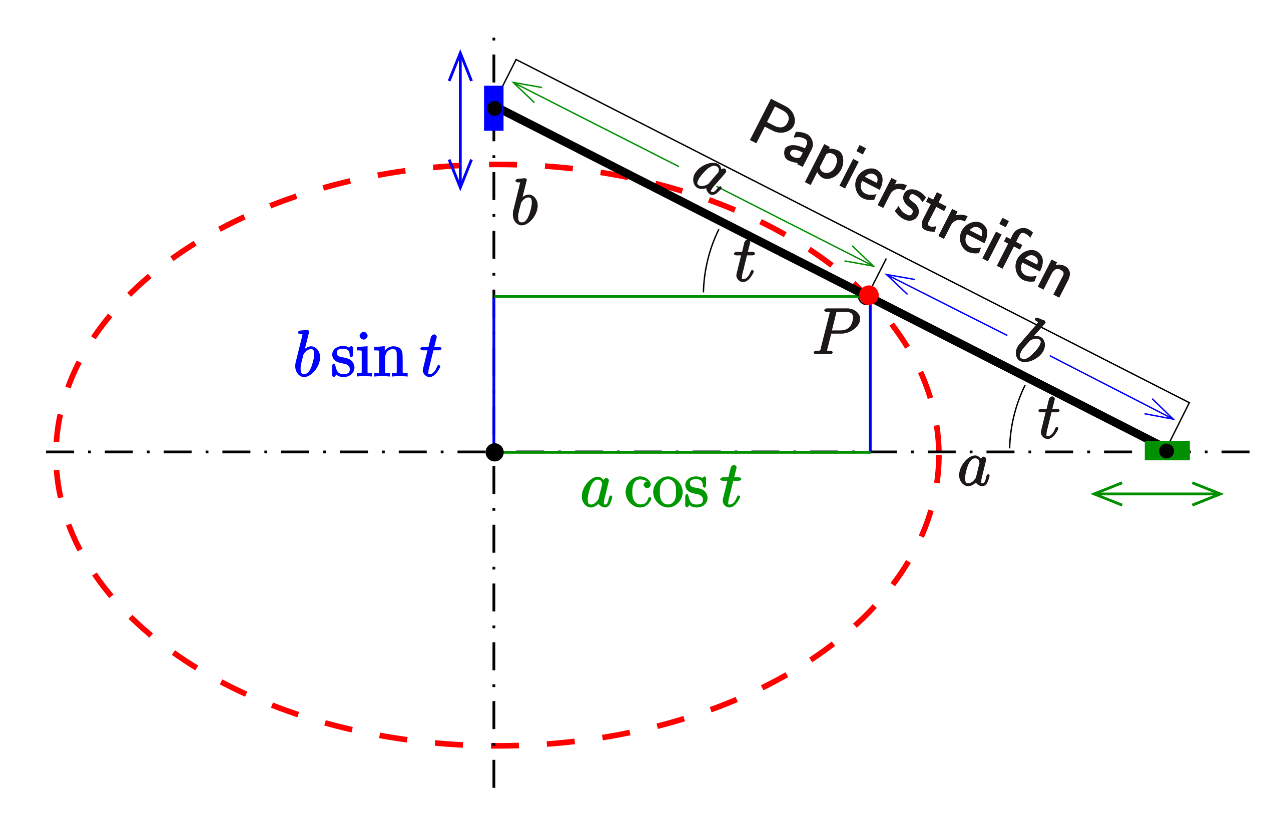
Ellipse: 1. Papierstreifenmethode
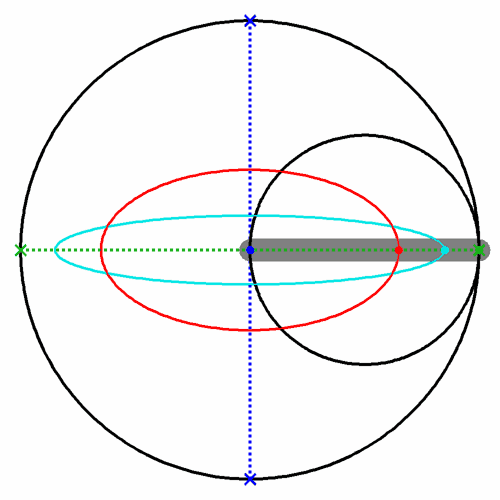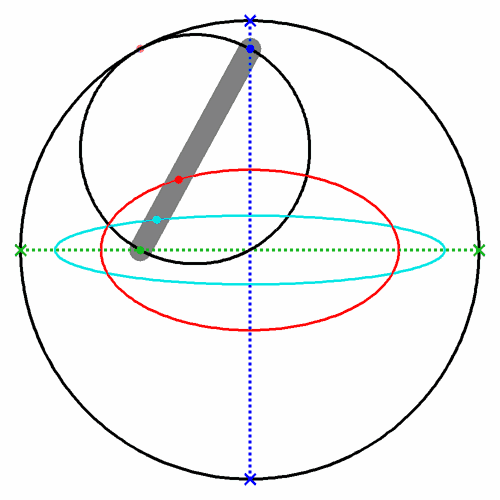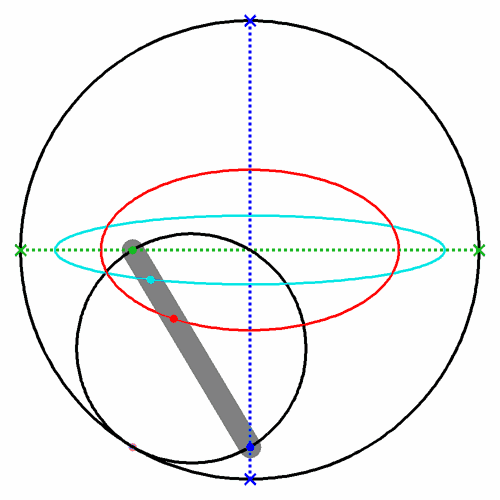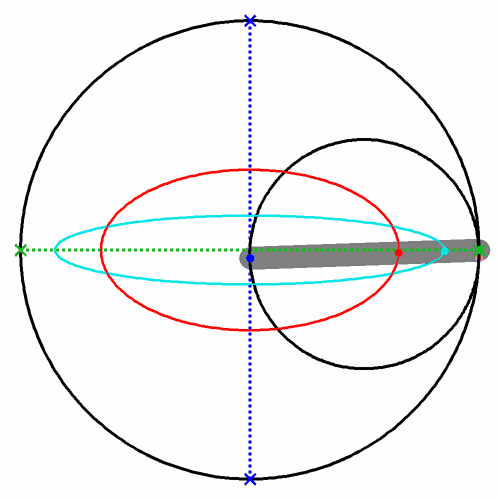
Ellipsen (rot, cyan) mit cardanischen Kreisen
.
Eine Variation der 1. Papierstreifenmethodegeht von der Beobachtung aus, dass der Mittelpunkt 
des Papierstreifens sich auf dem Kreis mit Mittelpunkt 
und Radius 
bewegt. Man kann also den Papierstreifen in der Mitte (Punkt ) trennen und an dieser Stelle ein Gelenk einfügen und den zuvor auf der 
-Achse gleitenden Punkt in den Mittelpunkt der Ellipse verlegen. Nach dieser Operation bleibt das abgeknickte Ende des Papierstreifens fest (im Punkt ) und der unveränderte Teil des Streifens samt dem Punkt 
bewegt sich wie zuvor. Der Vorteil dieser Variation ist: Man benötigt nur einen technisch anspruchsvollen Gleitschuh. Auch gegenüber der cardanischen Realisierung der 1. Papierstreifenmethode ist diese Variation technisch einfacher.
Man beachte, dass immer dasjenige Ende des Streifens, das auf der Nebenachse gleitet, in den Mittelpunkt verlegt wird!
des Papierstreifens sich auf dem Kreis mit Mittelpunkt und Radius bewegt. Man kann also den Papierstreifen in der Mitte (Punkt ) trennen und an dieser Stelle ein Gelenk einfügen und den zuvor auf der -Achse gleitenden Punkt in den Mittelpunkt der Ellipse verlegen. Nach dieser Operation bleibt das abgeknickte Ende des Papierstreifens fest (im Punkt ) und der unveränderte Teil des Streifens samt dem Punkt bewegt sich wie zuvor. Der Vorteil dieser Variation ist: Man benötigt nur einen technisch anspruchsvollen Gleitschuh. Auch gegenüber der cardanischen Realisierung der 1. Papierstreifenmethode ist diese Variation technisch einfacher.
Man beachte, dass immer dasjenige Ende des Streifens, das auf der Nebenachse gleitet, in den Mittelpunkt verlegt wird!Abgeknickter Papierstreifen
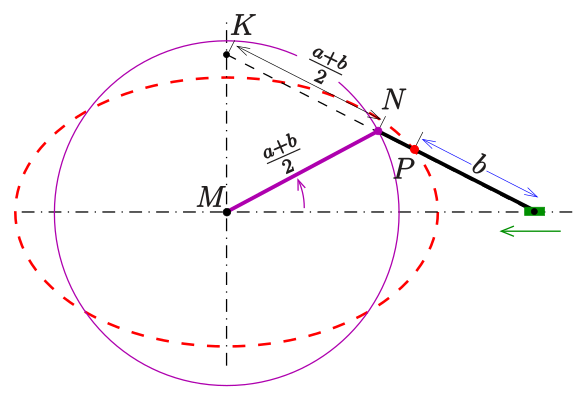
Animation mit abgeknicktem Papierstreifen
