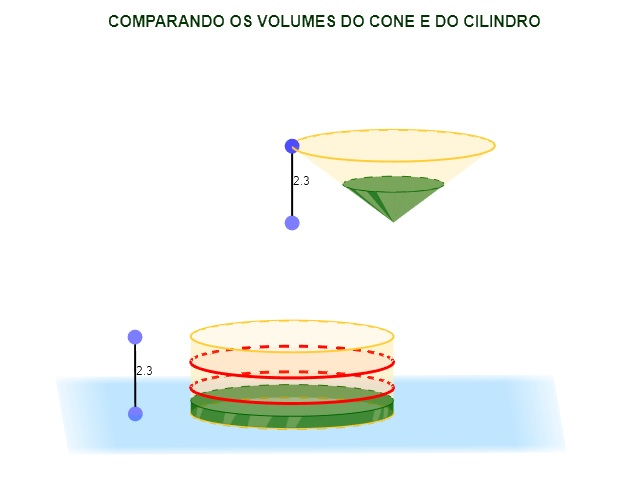
COMPARANDO OS VOLUMES DO CONE E DO CILINDRO
O applet desta postagem tem apenas efeito visual, serve para a observação intuitiva de que o volume de um cone equivale a 1/3 do volume de um cilindro com mesma altura e mesma área circular na base.
Antes de começar a atividade de observação, peça que movam a vontade os controles (r) e (h), que alteram a área da base e a altura dos dois sólidos, é importante que notem que a altura dos dois sólidos são congruentes, assim como a área circular na base deles. Depois dessas explorações segue a próxima tarefa...
Na verdade o cone é um recipiente cônico supostamente cheio de um líquido verde que deverá despejado no recipiente cilíndrico que está claramente vazio. Isso é feito movendo o controle (e) para o valor zero, feito isso a turma observará que todo o líquido verde após passado para o recipiente cilíndrico, a superfície do líquido chega somente até a primeira marca vermelha no recipiente, que marca exatamente 1/3 de toda a capacidade deste recipiente. Você deve levantar quiestionamentos com a turma, deixe exporem suas opiniões, depois levante a pergunta: " Se mudarmos a altura dos dois recipientes, ou a área de suas bases, será que o líquido continua enchendo apenas 1/3 do recipiente cilíndrico?
Então peça que retornem o valor do controle (e) para 1 e façam novamente outras modificações na área das bases e nas alturas simultaneamente. Depois zerem novamente o controle (e). Eles verão que o líquido continua preenchendo apenas até a linha que marca 1/3. Diga à turma que façam agora alterações com o recipiente cilíndrico contendo o lîquido, eles verão que mesmo alterando a área da base e a altura, o nível não sai da marcação. Levante questionamentos e depois conclua que SEMPRE, o volume de um cone terá 1/3 do valor do volume de um cilindro de mesma altura e mesma área circular de base, se quiser pode aplicar no quadro a prova matemática para essa observação e exercícios para fixação do conteúdo.