Example
Young's Inequality is a mathematical inequality that relates the convolution of two functions to their individual norms. It is useful in various mathematical and engineering contexts, especially in functional analysis and signal processing. Young's Inequality is expressed as follows:
Let f and g be two real-valued functions defined on the real line, and let p, q, and r be positive real numbers such that:
1/p + 1/q = 1 + 1/r
Then, for any real numbers 'a' and 'b', the following inequality holds:
|a * b| ≤ (|a|^p / p) + (|b|^q / q)
where:
|a| denotes the absolute value of 'a'.
**Examples:**
1. Using Young's Inequality to Bound the Convolution:
Suppose we have two functions f(x) = x^2 and g(x) = x^3 on the interval [0, 1]. We want to find an upper bound for their convolution h(x) = ∫[0, 1] f(t) * g(x - t) dt.
Using Young's Inequality with p = 2, q = 3, and r = 6 (since 1/2 + 1/3 = 1 + 1/6), we get:
|h(x)| ≤ (|f(x)|^2 / 2) + (|g(x)|^3 / 3)
|h(x)| ≤ (x^4 / 2) + (x^9 / 3)
So, the upper bound for the convolution h(x) is given by (x^4 / 2) + (x^9 / 3).
2. Estimating a Signal Processing Operation:
Young's Inequality is also used in signal processing to estimate operations like the convolution of two signals. Let's say we have a signal 'x(t)' and a filter 'h(t)' in the time domain, and we want to compute their convolution y(t) = x(t) * h(t).
Using Young's Inequality with appropriate values of p, q, and r, we can estimate the magnitude of the output signal 'y(t)'.
For example, if we take p = 1, q = 1, and r = 1 (since 1/1 + 1/1 = 2), then we get:
|y(t)| ≤ |x(t)| + |h(t)|
This means that the magnitude of the output signal 'y(t)' is bounded by the sum of the magnitudes of the input signal 'x(t)' and the filter 'h(t)'.
Young's Inequality provides a powerful tool for understanding and analyzing various mathematical and engineering problems that involve convolutions and norms. It allows us to derive upper bounds for certain expressions involving functions, which can be very useful in theoretical analysis and practical applications.
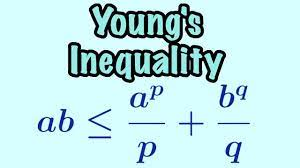
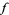 be a real-valued, continuous, and strictly increasing function on
be a real-valued, continuous, and strictly increasing function on 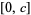 with
with 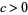 . If
. If 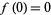 ,
, 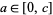 , and
, and 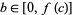 , then
, then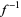 is the inverse function of
is the inverse function of 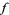 . Equality holds iff
. Equality holds iff 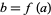 .Taking the particular function
.Taking the particular function 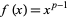 gives the special case
gives the special case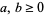 ,
, 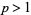 , and
, and