El teorema de la suma de dos sucesiones límite
Teorema: Si dos secuencias son convergentes, entonces su suma es convergente; El límite de la suma es igual a la suma de los límites
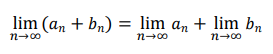
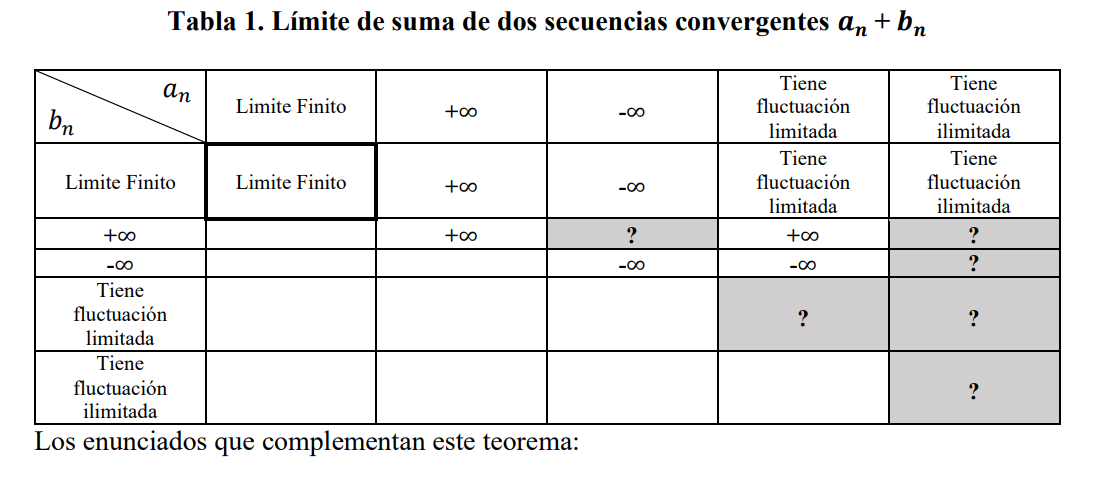
Al formular los teoremas básicos sobre el límite de sucesiones (particularmente el teorema sobre la suma de dos sucesiones convergentes), es necesario crear una serie de enunciados de apoyo que explique sustancialmente todos los casos importantes de representación de componentes límite (para el teorema mencionado (negrita del cuadrado de Tabla 1) – siete declaraciones en las que se revisan casos de representación límite para cada uno de los componentes). La implementación de esta información en la tabla con dos entradas (Tabla 1) brinda la oportunidad no solo de organizar esa información, sino también de brindar a los estudiantes apoyo para la aplicación del conocimiento en situaciones estándar y no
estándar, particularmente para comprender el origen de las incertidumbres.

En particular, el registro en la segunda fila y la segunda columna de la tabla (en el cuadrado resaltado) refleja el contenido del teorema fundamental. La información de la segunda fila se desarrolla: si tiene un límite finito, entonces la suma se comporta como el segundo término. La parte en blanco de la mesa es simétrica a la diagonal principal. Las celdas completas de la tabla están presentes donde el comportamiento de la suma de dos secuencias es obvio. Todos los casos deben consistir en enunciados que complementen el teorema básico.