Classificação de Triângulos
Quanto aos lados
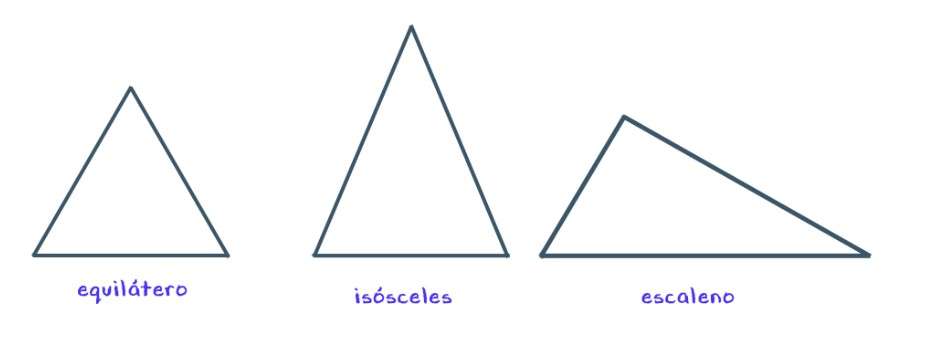
- Equiláteros: possuem os três lados congruentes (e, consequentemente, os três ângulos também). Para todo triângulo equilátero, os ângulos possuem sempre a mesma medida: 60°; - Isósceles: possuem dois lados congruentes (e, consequentemente, dois ângulos também) – o terceiro lado é chamado base e o ângulo oposto à base é o ângulo do vértice; - Escalenos: não possuem quaisquer lados congruentes (e, consequentemente, os ângulos também não são congruentes).
Quantos aos ângulos
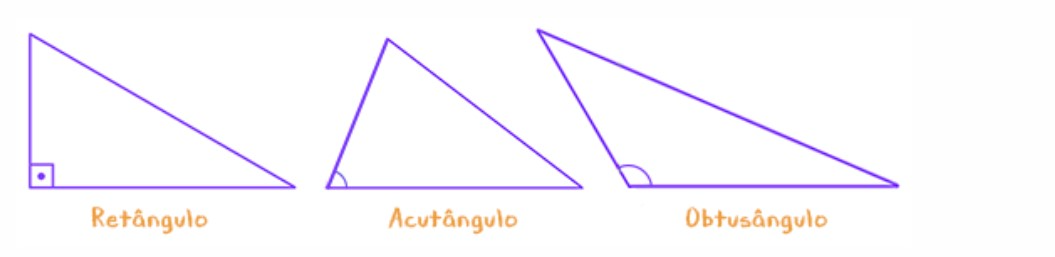
- Retângulos: possuem um ângulo reto (o lado oposto ao ângulo reto de um triângulo retângulo é sua hipotenusa e os outros dois são os catetos do triângulo); - Acutângulos: possuem os três ângulos agudos; - Obtusângulos: possuem um ângulo obtuso.
Exemplos:
Faça alguns triângulos, e veja qual é a sua classificação. (Mudando de posição os pontos A,B e C)
Faça um triângulo equilátero.
Questão 1
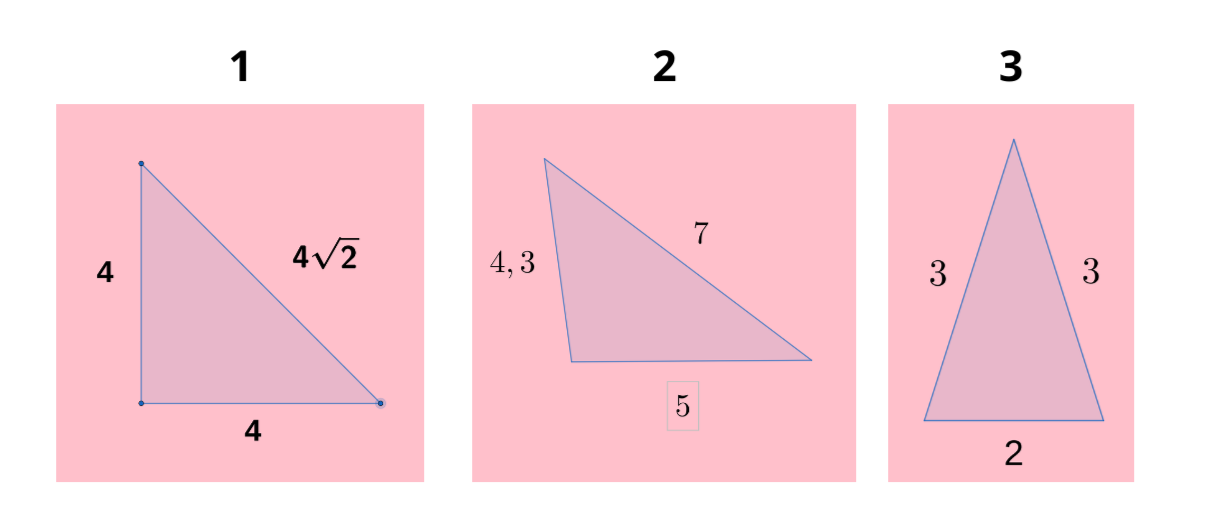
Qual dos triângulos abaixo NÃO é isósceles?
Questão 2
Avalie as afirmações abaixo, e indique quais são as verdadeiras. a) Todo triângulo isósceles é equilátero. b) Todo triângulo equilátero é isósceles. c) Todo triângulo retângulo é escaleno. d) Existe triângulo retângulo isósceles. e) Todos os triângulos equiláteros apresentam as medidas dos lados e dos ângulos congruentes. f) O triângulo equilátero apresenta um ângulo obtuso. g) Todo triângulo acutângulo é isósceles. h) Um triângulo que tem um ângulo reto é necessariamente um triângulo acutângulo. i) Um triângulo escaleno pode ter um ângulo reto. j) O triângulo obtusângulo pode ser isósceles.
Questão 3
Das afirmativas da questão anterior, justifique as falsas.