Die Scheitelpunktform einer quadratischen Funktion
Kurzinformation:
Thema: quadratische Funktionen
Mathematik an Gymnasien in Baden Württemberg, 8. Klasse
Dauer: 90 Minuten ( eine Doppelstunde)
Spezielle Materialien: Computer mit Geogebra- Zugang
Didaktische Herangehensweise an die Scheitelpunktform einer quadratischen Funktion
Oft haben Schüler*innen in der Schule bereits große Schwierigkeiten, den allgemeinen Funktionsbegriff voll und ganz zu verstehen, weshalb bereits von Anfang an Fehlvorstellungen bei Schüler*innen gebildet werden, beispielsweise der "Graph als Bild Fehler", bei der der Graph als unmittelbares fotographisches Abbild einer Situation angesehen wird und dadurch zum Beispiel einem Skifahrer wie hier gezeigt der darunter abgebildete Geschwindigkeitsgraph zugeordnet wird:

Doch selbst, wenn Schüler*innen diese Fehlvorstellung umgangen sind, gibt es noch viele weitere, gerade auch, wenn von linearen Funktionen zu quadratischen Funktionen übergegangen wird.
So neigen wir zum Beispiel oft dazu, alles zu Linearisieren, auch wenn man eigentlich beispielsweise quadrieren muss. Auch fällt es den Schüler*innen schwer, die Funktion als Ganzes zu betrachten, was beim Arbeiten mit quadratischen Funktionen allerdings große Bedeutung hat, da diese oft auf Symmetrie und darauf angewandte Transformationen untersucht werden. Weitere Fehlvorstellungen liegen darin, zu denken, das Quadrieren hätte immer ein Wachstum zur Folge und alles, wovor ein plus steht und die Wirkung hat, dass der Graph verschoben wird, verschöbe diesen in eine positive Richtung, sodass beispielsweise der Graph zu der Funktionsgleichung f(x)=(x+3)² Folgener ist:
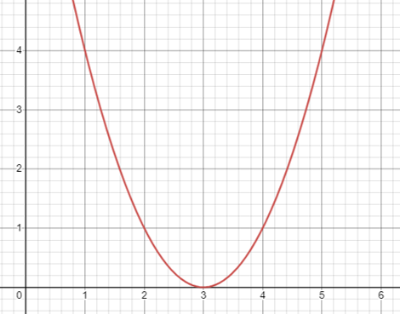
Dies ist natürlich schlichtweg falsch.
Um solch gravierende Fehlvorstellungen wie oben genannt zu umgehen, ist es an zentraler Bedeutung, dass Lehrkräfte das didaktische Prinzip "Didaktische Reduktion" anwenden. Hierbei werden die Unterrichtsmaterialen so aufgearbeitet, dass sie für die Schüler*innen verständlich, jedoch noch fachlich richtig und ausbaufähig sind. Dies kann entweder durch Reduktion des Umfangs oder der Schwierigkeit geschehen (vertikal) oder indem man den Unterrichtsinhalt gleich lässt, jedoch das zu Lernende durch anschauliche Darstellungen lehrbar macht (horizontal). Letzteres ist vor allem wichtig für uns Lehrkräfte, wenn wir eben diesen Lernstoff vermitteln müssen und weder am Umfang, noch an der Schwierigkeit dessen etwas verändern können. Große Helfer hierbei sind die digitalen Werkzeuge, die uns zur Verfügung stehen, wie beispielsweise Geogebra. Lernen die Schüler*innen den neuen Lerninhalt nach dem Prinzip des entdeckenden Lernens zudem selbst kennen, wird dieser noch mehr verinnerlicht und wird somit nicht mehr schnell vergessen.
Mithilfe von Geogebra kann zum Beispiel der Zusammenhang zwischen der Lage des Graphen und den Parametern in dem jeweiligen Funktionsausdruck hergestellt werden.
Ziel der folgenden Einheit:
Die Schüler*innen sollen in dieser Einheit an die Scheitelpunktform einer quadratischen Funktion
herangeführt werden, indem hier zuerst einmal die Verschiebung einer Parabel durch Verändern der
Parameter d und e in der Form f(x)=(x-d)²+e nahegebracht wird.
Vorgehobene Didaktische Prinzipien zu dieser Unterrichtseinheit:
Didaktische Reduktion:
vertikal:
Die Stauchung und Streckung der Parabel wird zunächst nicht thematisiert, um eine Überforderung der
Schüler*innen zu vermeiden.
horizontal:
Mithilfe von Geogebra werden die Änderungen des Graphen bei Veränderung der Funktionsgleichung
sofort durchgeführt, sodass die jeweiligen Auswirkungen für die Schüler*innen sofort anschaulich werden.
Entdeckendes Lernen:
Durch die selbst entdeckten Zusammenhänge zwischen Funktionsgleichung und zugehörigem
Graphen, soll der obigen Fehlvorstellung der Verwirrung, in welche Richtung der Graph bei
Verändern des Parameters d in der Form f(x)= (x-d)²+e verschoben wird, so gut es geht entgegengewirkt
werden.
Die Schüler*innen kennen zu dem Zeitpunkt bisher Folgendes:
- Allgemeines rund um Funktionen ( Was Funktionen, Funktionsgleichungen sind; Einzeichnen von Punkten
oder Graphen mithilfe von Wertetabellen in ein Koordinatensystem; Darstellungswechsel zwischen den vier
Darstellungsformen: der situativ- sprachlichen, der numerisch- tabellarischen, der graphisch- visuellen
und der formal- symbolischen)
- die Quadratzahlen von 1 bis 20
- die Normalparabel mit der Funktionsgleichung f(x)=x²
- der Scheitelpunkt einer Parabel
Ablauf der Unterrichtseinheit
Jeder der ersten drei Arbeitsaufträge wird mit einem Arbeitsaufwand von 15 Minuten berechnet. Je im
Anschluss der ersten drei Arbeitsaufträge wird zusammen ein Regelheftaufschrieb mithilfe der
Vorschläge der Schüler*innen erarbeitet, für das nochmal jeweils 10 Minuten eingeplant werden, um
aufkommende fehlerhafte Vorstellungen schnellstmöglich zu beseitigen und alle Schüler*innen auf
dieselbe Aufgabe zu bringen.
Ziel ist, dass die ersten 3 Teilaufgaben der Übungsaufgabe zusammen im Unterricht in den letzten 10
Minuten besprochen werden (5 Minuten für die Schüler*innen zum Bearbeiten und 5 Minuten zum
Besprechen und zur Klärung der letzten Fragen), um mögliche Missverständnisse zu der Aufgabe bereits
im Unterricht zu beseitigen. Die restlichen Teilaufgaben werden als Hausaufgabe aufgegeben.
6 Minuten werden für das Hoch- und Herunterfahren der Computer, sowie Organisatorisches berechnet.
Sicherung:
Der nach den ersten drei Arbeitsaufträgen jeweils zusammen formulierte Regelheftaufschrieb, wird von den
Schüler*innen in ihr jeweiliges Regelheft abgeschrieben.
Überprüfung des Lernerfolges
In den Besprechungsphasen nach den einzelnen Arbeitsaufträgen wird überprüft, inwieweit die
Schüler*innen den jeweils erarbeiteten Zusammenhang verstanden haben und abstrahieren
können. Durch die schriftlich festgehaltenen Formulierungen, die mithilfe der anderen
Schüler*innen und der Lehrkraft gegebenenfalls korrigiert werden, wird zudem die fachlich
korrekte Sprache gefördert und kann für die Lehrkraft nochmals als Einschätzung dienen, inwieweit
die Schüler*innen mit mathemaischen Grundbegriffen umgehen können.
Bei der Besprechung der ersten Teile der Übungsaufgabe wird zudem überprüft, wer bereits jetzt
das eben Erlernte auf konkrete Beispiele anwenden kann.
In der nächsten Stunde wird am Anfang der Rest der Hausaufgabe besprochen. Hierbei werden auch
Schüler*innen aufgefordert, die in der vorherigen Stunde eher wenig bis nichts gesagt haben.
1. Arbeitsauftrag
Parabeln können durch Verändern der Funktionsgleichung im Koordinatensystem in beliebige Richtung verschoben werden, so zum Beispiel nach oben und nach unten.
Verschiebe den Scheitelpunkt der angezeigten Parabel und beobachte hierbei Folgendes:
Wie verändert sich die Funktionsgleichung, wenn man den Scheitelpunkt nach oben oder nach unten
verschiebt?
Leite zusammen mit deinem Sitznachbar eine Regel ab (schriftlich), die diesen Zusammenhang beschreibt.
2. Arbeitsauftrag
Die Parabel kann zusätzlich nach links und nach rechts verschoben werden.
Gehe hierbei analog wie oben vor. Verschiebe also wieder den Scheitelpunkt der Parabel, diesmal nach links und rechts und beobachte, wie sich nun die Funktionsgleichung der Parabel verändert.
Leite hierbei in Partnerarbeit eine Regel zum Zusammenhang zwischen Funktionsgleichung und Verschiebung der Parabel zur Seite ab (schriftlich).
3. Arbeitsauftrag
Eine Parabel kann auch sowohl zur Seite, als auch nach oben, bzw. unten verschoben werden.
Verschiebe die unten stehende Parabel also in eine beliebige Richtung. (Wieder durch Anklicken des Scheitelpunktes)
Welchen Zusammenhang fällt dir zwischen der Funktionsgleichung und dem Scheitelpunkt der Parabel auf?
Stelle mit deinem Sitznachbar eine Regel hierfür auf (schriftlich).
Übungsaufgabe
Die Parabel verfärbt sich bei Verschieben.
Ordne den folgenden Funktionsausdrücken den Farben rot, grün, dunkelblau, hellblau gelb und violett zu ( Mehrfachnennungen möglich).
i) f(x)= x²
ii) g(x)= x²+3
iii) h(x)= (x+1)²
iv) i(x)= (x-3)²-1
v) j(x)= (x+2)+2
vi) k(x)= (x+3)²-1
vii) l(x)= (x-1)²+2
viii) m(x)= x²-1
ix) n(x)= (x-4)²
x) o(x)= (x-3)²+1
Um eine solche Parabel mit wechselnder Farbe zu erstellen, folgen Sie der Anleitung, die bereits ähnlich in dem Praktikum zur Präsentation "Quadratische Funktionen und Potenzfunktionen" geschrieben ist:
i) Erstellen Sie eine Parabel, deren Scheitelpunkt die Koordinaten (d,e) hat und dessen Funktionsausdruck die
Parameter d und e enthält, indem Sie "f(x)=(x-d)²+e in die Eingabeleiste eingeben. Erstellen Sie für jeden
Parameter nun noch je einen Schieberegler.
Sollte Geogebra e nicht als Parameter anerkennen, erstellen Sie zunächst einen Schieberegler für
einen Parameter c, benennen Sie diesen dann um in e und schreiben erst im Anschluss die
Funktionsgleichung in die Eingabeleiste.
ii) Erstellen Sie einen Punkt S mit den Koordinaten (d,e), indem Sie S=(d,e) in der Eingabeleiste eingeben.
iii) Verändern Sie nun je nach Lage die Farbe des Graphen. Folgen Sie hierzu folgender Anleitung:
1. Öffnen Sie die Einstellungen der Parabel.
2. Drücken Sie nun auf "Erweitert" ganz oben rechts.
3. Unter "Dynamische Farben" stehen "Rot", "Grün", "Blau". Geben Sie neben "Rot:" "d == 0|| e == 0",
neben "Grün:" "d<0||e<0" und neben "Blau:" "d>0||e>0" ein.
"||" übersetzt Geogebra mit "oder" und "==" mit einem Gleichheitszeichen.
iv) Achten Sie im Anschluss darauf, dass zum Schluss der Punkt S in der Algebra- Ansicht angeklickt ist,
damit sich die Lage des Graphen durch Verschieben des Scheitelpunktes verändert.
Damit die Algebra- Ansicht für die Schüler*innen nicht sichtbar ist, achten Sie darauf, dass beim
Anklicken von "Erweiterte Einstellungen" für das Geogebra- Applet ganz unten lediglich ein Haken
bei "Bewegungen der Ansicht und Zoom aktivieren" gesetzt ist.
