Definizione di funzione numerica e di grafico
Le funzioni numeriche
Particolarmente importanti in matematica sono le funzioni numeriche.
Si ha una funzione numerica quando i due insiemi A e B sono numerici (di solito sottoinsiemi di R).
In questo caso gli elementi di A e B vengono chiamati variabili (rispettivamente indipendenti e dipendenti).
Le funzioni numeriche possono essere funzioni empiriche o funzioni matematiche.
Le funzioni matematiche sono quelle nelle quali la legge che associa gli elementi di A a quelli di B è descrivibile mediante una espressione analitica (cioè attraverso operazioni matematiche).
In questo caso si dice che y = f(x) è l’equazione della funzione.
Assegnata una funzione matematica di equazione y = f(x), definita nell’insieme A ed a valori nell’insieme B, si definisce grafico della funzione l’insieme di tutti i punti P(x,y) del piano cartesiano tali che x appartiene ad A e y = f(x).Quindi un punto P(x,y) appartiene al grafico di una funzione se e solo se le sue coordinate soddisfano l'equazione della funzione.
Se la nostra funzione ha equazione:
y = 2x + 5
Leggendo attentamente un grafico si possono dedurre tutte le proprietà
di una funzione pur non conoscendone la legge.
OSSERVA
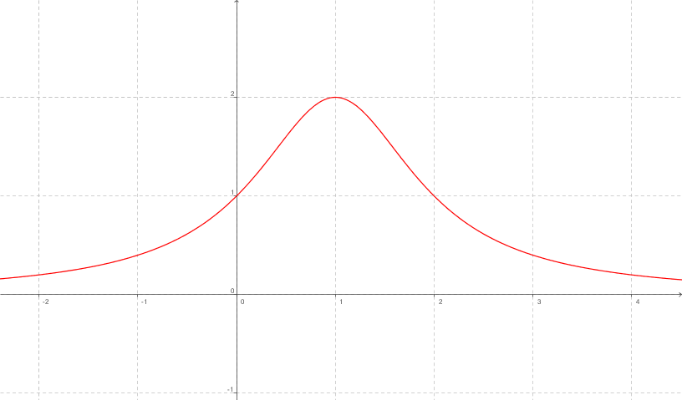
quanto vale f(1)?
e f(0)?
Qual è la preimmagine del 2?