Natürliche Exponentialfunktion: Verhalten an den Rändern des Definitionsbereichs
Motivation: Besonderheit beim Grenzwertverhalten der natürlichen Exponentialfunktion
Wir haben eben im Unterricht festgestellt, das gilt:

Interessant ist die Frage, gegen welchen Grenzwert verkettete Funktionen streben.
Wir betrachten dazu die Funktion mit .
Grenzwertverhalten einer Bruch-Funktion
Bevor wir uns genauer ansehen, wie der Grenzwert von g bestimmt werden kann, sollten wir uns überlegen, wann der Wert eines Bruchs sehr groß wird oder gegen 0 strebt. Wähle die richtigen Aussagen aus. (Wir gehen davon aus, dass der Wert von Zähler und Nenner stets positiv ist.)
Was bedeutet das für das Grenzwertverhalten der Funktion g?
Betrachten wir wieder . Gegen welchen Wert strebt g, wenn x gegen unendlich strebt?
Allein durch die Betrachtung, die wir oben für Brüche gemacht haben, lässt sich das nicht entscheiden. Sowohl der Zähler als auch der Nenner von g streben gegen unendlich. Aus der Betrachtung von oben müsste dann sowohl der Bruch gegen 0 als auch gegen unendlich streben.
Und jetzt kommt die Besonderheit ins Spiel, die bei der natürlichen Exponentialfunktion vorliegt:
Funktionen, die alle den Grenzwert unendlich haben, unterscheiden sich darin, wie "schnell" sie gegen unendlich streben.Unsere natürliche Exponentialfunktion ist nun nicht nur diejenige Funktion, die ihre eigene Ableitungsfunktion ist, sondern sogar auch noch die Funktion, die schneller gegen unendlich wächst als jede Potenz .
Wir wissen also jetzt, dass der Nenner des Funktionsterms von g schneller gegen unendlich strebt, als der Zähler. Es stellt sich die Frage:
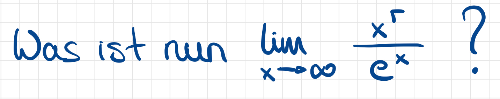
Wähle den passenden Grenzwert aus.
Grenzwertverhalten von g am Graphen von g erkennen.
Überzeuge dich auch anhand des Funktionsgraphen von g davon, dass der Grenzwert von g für x gegen unendlich gleich 0 ist. Variiere dafür den Schieberegler für den Wert des Exponenten r und beobachte den Verlauf des Graphen von g (blau) für x gegen unendlich.
Zusammenfassung
Formuliere in eigenen Worten, wie die besondere Eigenschaft im Grenzwertverhalten der natürlichen Exponentialfunktion (wächst schneller als jede Potenz) und das Grenzwertverhalten der Funktion g (Graph oben) zusammenhängen.