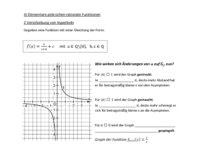
Parameter gebrochen-rationaler Funktionen
Lernziele:
die "Normalhyperbel" mit ihren Eigenschaften definieren
die allgemeine Funktionsgleichung einer gebrochen-rationalen Funktion mit den Parametern a, b und c
aufstellen
die Auswirkungen von Veränderungen der Parameter auf die Lage und Streckung des Graphen
beschreiben
mithilfe der Parameter Graphen zu gegebenen Termen skizzieren
Funktionsterme elementarer gebrochen-rationaler Funktionen zu gegebenen Graphen aufstellen

Diesmal beginnen wir sofort mit dem Hefteintrag (bitte die Formeln, obwohl sie schwarz dargestellt werden, mit abschreiben! Die Farbe lässt sich nicht ändern!):
III.2 Verschiebung von Hyperbeln
Man kann den Graphen der Funktion als Normalhyperbel bezeichnen.
Sie …
hat die Koordinatenachsen als Asymptoten,
ist punktsymmetrisch zum Koordinatenursprung
ist achsensymmetrisch zu den Winkelhalbierenden der Koordinatenachsen
und
verläuft durch die Punkte (1|1) und (-1|-1).
(Bild siehe unten; am besten an dieser Stelle auch ins Heft übernehmen!)
Allgemein hat eine gebrochen-rationale Funktion jedoch die Form
mit \{0} und , .
Hierbei bezeichnet man , und als Parameter (altgr. „Nebenmaß“) der Funktion. Sie bestimmen Lage und Streckung der Funktion im Vergleich zur Normalhyperbel.
![[size=100]"Normalhyperbel"[/size]](https://www.geogebra.org/resource/tv6w6fh9/Pvau77I682uZVI9g/material-tv6w6fh9.png)

Aufgabe:
Verändere die Werte der Parameter mithilfe der Schieberegler und beobachte, wie sie sich auf den Verlauf des Graphen auswirken. Wie verändert sich der Graph im Vergleich zur Normalhyperbel?
Fasse deine Beobachtungen auf dem Arbeitsblatt zusammen, zeichne die Graphen der angegebenen Funktionen farbig in die drei Koordinatensysteme und vergleiche anschließend mit der Lösung auf dem Tisch vorne beim Lehrerpult.
III_2_Verschiebung von Hyperbeln_Arbeitsblatt
Übung: S. 66/4
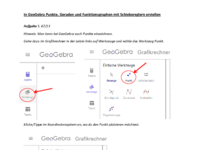
Nutze zur Lösung einfach das obige GeoGebra-Applet! Falls das nicht gehen sollte, öffne den folgenden Link in einem neuen Tab: Grafikrechner und kopiere diesen Ausdruck ins Eingabefeld: f(x)=a/(x+b)+c

Notiere dir die Werte für a, b und c jeweils bitte auch in dein Heft!
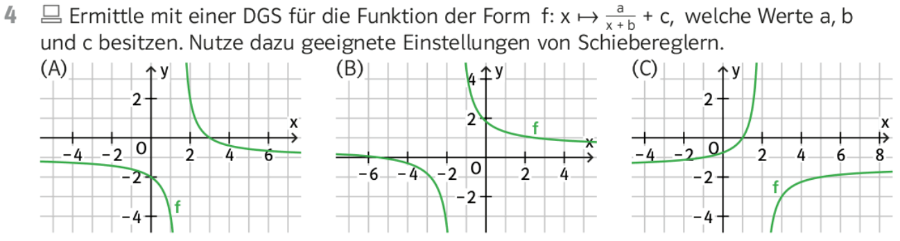
Lösung zur Selbstkontrolle hier:
Übung: S. 66/8a - e
Gib zur Funktion die Gleichungen der waagrechten und senkrechten Asymptote an. Die Lösungen kannst du selbstständig kontrollieren.
a) :
b) :
c) :
d) :
e) :

NÜTZLICH:
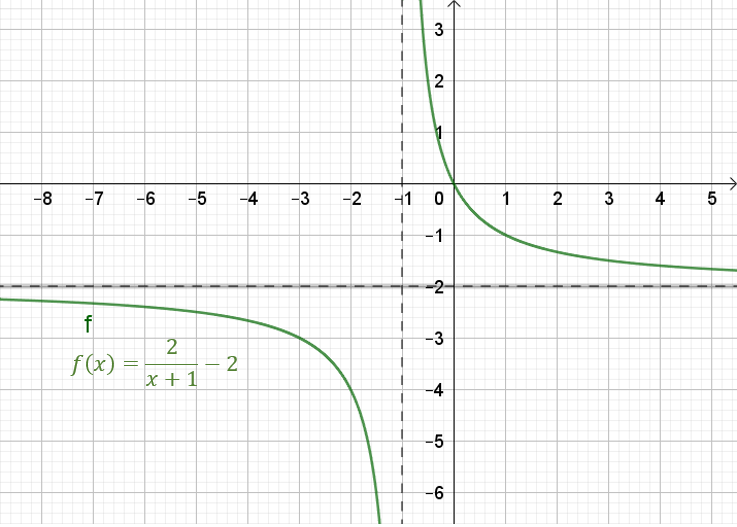
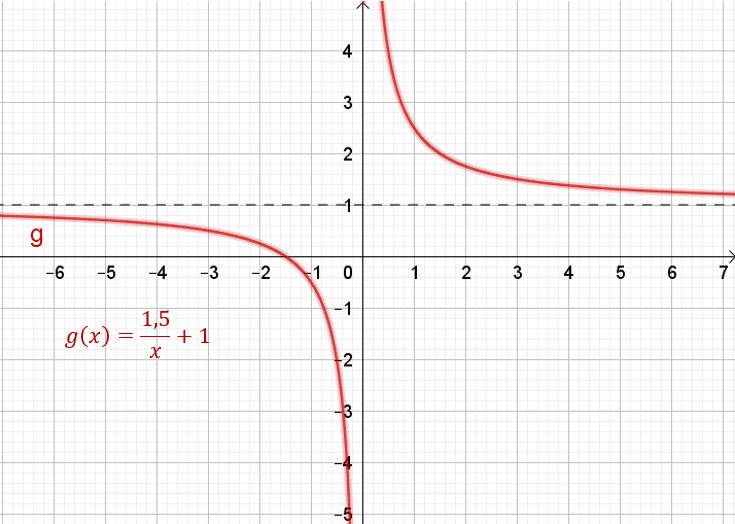
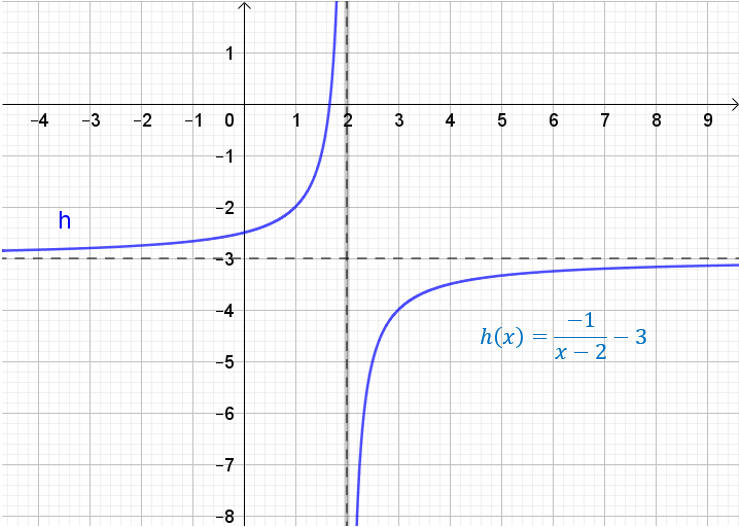
Versuche bei den Graphen unten einmal Folgendes:
1) Suche den Schnittpunkt der Asymptoten.
2) Bewege dich von dort um eine LE nach rechts. Wie viele LE musst du nun nach oben gehen, um den
Graphen zu erreichen? Notiere dir die Antwort für alle angegebenen Graphen neben dem
Funktionsterm.
(Musst du nach unten gehen, notiere dir vor die Anzahl LE ein Minus.)
3) Sieh dir deine Notizen an und vergleiche mit den Funktionstermen. Fällt dir ein Zusammenhang mit
einem der Parameter auf?
Fasse deine Erkenntnis folgendermaßen in deinem Heft zusammen:
| Schnittpunkt der Asymptoten → 1 Schritt nach rechts ↑ _______ Schritte nach oben. |
Hinweis:
Hier musst du nichts eingeben, lass dir einfach die Antwort anzeigen.
Einfach anzeigen lassen, um herauszufinden, was in die Lücke oben muss!
Übung: S. 67/13a, b
Hierzu kannst du wieder den Grafikrechner mit Schiebereglern nutzen, indem du f(x)=a/(x+b)+c in das Eingabefeld kopierst oder eintippst.
Du kannst aber auch dein gesammeltes Wissen über gebrochen-rationale Funktionen und ihre Parameter nutzen, um dir einen Funktionsterm zusammenzubasteln.