Angoli al centro e angoli alla circonferenza
Si dice angolo alla circonferenza un qualsiasi angolo il cui vertice appartiene alla circonferenza. I lati di un angolo alla circonferenza possono essere
- entrambi secanti (sono semirette che hanno origine nel vertice dell'angolo e intersecano la circonferenza in un altro punto)
- uno secante e l'altro tangente (semiretta che ha origine nel vertice dell'angolo e non interseca la circonferenza in altri punti)
Costruisci due circonferenze: in una traccia un angolo alla circonferenza con lati secanti e nell'altra un angolo alla circonferenza con un lato secante e uno tangente.
Un angolo alla circonferenza ed un angolo al centro (vertice nel centro) che insistono sullo stesso arco di circonferenza si dicono corrispondenti.
Muovi i punti A, B, C, D e osserva come cambiano le ampiezze degli angoli.
1) Dato un arco di circonferenza, quanti angoli al centro insistono su quell'arco? 2) E quanti angoli alla circonferenza? 3) Come sono tra loro gli angoli alla circonferenza che insistono sullo stesso arco? 4) Quale legame intuisci tra l'ampiezza dell'angolo al centro e di un angolo alla circonferenza corrispondente? 5) Quanto sono ampi l'angolo al centro e gli angoli alla circonferenza che insistono su una semicirconferenza (A e B estremi di un diametro)?
Disegna una circonferenza e due punti A e B sulla circonferenza: individui così due archi di circonferenza. Costruisci un angolo alla circonferenza su ciascuno dei due archi e misurane l'ampiezza.
Qual è il legame tra gli angoli alla circonferenza che insistono su due archi di circonferenza "complementari" (i due archi che individuano due punti A e B distinti sulla circonferenza)?
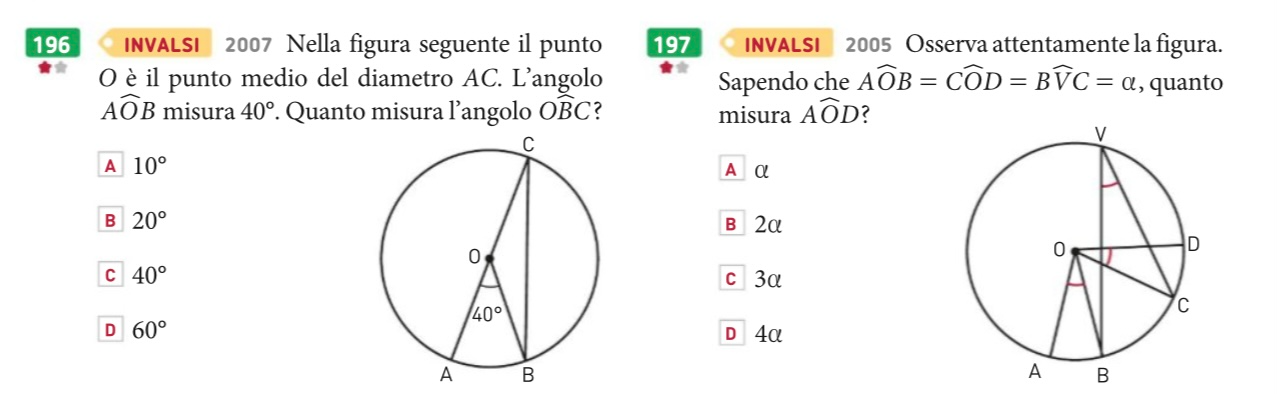
Risolvi qui gli esercizi giustificando le tue risposte.