Homogene Koordinaten Rotation um Achse
Konzept
Ein Element v ∈R3 kann sowohl als Punkt im Raum als auch als Richtungsvektor interpretiert werden. Das Konzept homogene Koordinaten stellt beide Objekte auch unterschiedlich dar als
Richtungsvektor oder Punkt im Raum
Mit A ∈ R3×3 ,eine Matrix, die eine lineare geometrische Transformation beschreibt, und v ∈ R3, ein Vektor lässt sich eine affine Transformation angeben
.
Sie ist die Verknüpfung einer linearen Transformation mit einer Verschiebung. Jede affine Transformation lässt sich in homogenen Koordinaten durch eine Matrix der Form
darstellen.
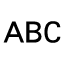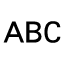http://www.math.kit.edu/iag2/~globke/media/koordinaten.pdf
Die Drehmatrix
Rn(,n1,n2,n3) =Drehwinkel, ni=Richtungsvektor (normiert) der Drehachse
TE=Translationsvektor für Punkt E (Für Drehung muss der Punkt in den Ursprung verschoben werden und nach der Drehung wieder zurück)
http://www.math.kit.edu/iag2/~globke/media/koordinaten.pdf
Die Drehmatrix
Rn(,n1,n2,n3) =Drehwinkel, ni=Richtungsvektor (normiert) der Drehachse
TE=Translationsvektor für Punkt E (Für Drehung muss der Punkt in den Ursprung verschoben werden und nach der Drehung wieder zurück)
Beispiel
Drehung um eine Achse im Raum. Gegeben durch einen Vektor v.
Beispiel in kartesischen Koordinaten und in homogenen Koordinaten:
Die Ecke einer Figur mit den Koordinaten
E = (5,8, -7)T
wurde um einen Winkel von pi/4 gegen den Uhrzeigersinn um die Drehachse v = 1/5(4,0,3)T gedreht.
Diese Richtung v entspricht der der Flächennormalen der Figur.
Zunächst soll die Ecke E und die Drehung in homogenen Koordinaten angegeben werden und dann die Transformationsmatrix M(Gesamt) in homogenen Koordinaten angegeben werden, die die Figur wieder in die ursprüngliche Position dreht.
AchsenDrehungenpi4
Beispiel in homogenen Koordinaten und Abbildung durch elementare Achsendrehungen Rx Ry Rz
Purgathofer, TU Wien (Link unten)
1. Schritt = Punkt P in den Koordinatenursprung verschieben: T(-px,-py,-pz)
2. Schritt = Vektor u in die z-Achse drehen
2a. Vektor u um die x-Achse in die xz-Ebene drehen: Rx(α)
Sei u = (a,b,c), dann ist u´=(0,b,c) die Projektion von u auf die yz-Ebene. Der Drehungswinkel α um die
x-Achse ergibt sich aus cos α = c/d mit d= √(b²+c²)
2b. Vektor u um die y-Achse in die z-Achse drehen: Ry(β)
Der Drehungswinkel β um die y-Achse ergibt sich aus cos β = d (bzw. sin β = -a)
3. Schritt = Drehung um θ um die z-Achse ausführen: Rz(θ)
4. Schritt = Vektor u in die ursprüngliche Richtung zurückdrehen: zuerst Ry(-β), dann Rx(-α)
5. Schritt = Punkt P1 an die ursprüngliche Position zurückverschieben: T(x1,y1,z1)
Rx(=0°) und Ry(=53.13°) bei Rz(=45°)