Igualdade de Triângulos
4.
Sejam os dois triângulos ABC, DEF, tendo os dois lados AB, AC iguais aos dois lados DE, DF, cada um a cada
um, por um lado, o AB ao DE, e, por outro lado, o AC ao DF, e o ângulo sob BAC igual ao ângulo sob EDF. Digo que também a base BC é igual à base EF, e o triângulo ABC será igual ao triângulo DEF, e os ângulos restantes serão iguais aos ângulos restantes, cada um a cada um, sob os quais se estendem os lados iguais, por um lado, o sob ABC ao sob o DEF e, por outro lado, o sob ACB ao sob DFE. Pois, o triângulo ABC, sendo ajustado sobre o triângulo DEF, e sendo posto, por um lado, o ponto A sobre o ponto D, e, por outro lado, a reta AB sobre a DE, também o ponto B se ajustará sobre o E, por ser a AB igual à DE; então, tendo se ajustado a AB sobre a DE, também a reta AC se ajustará sobre a DF, por ser o ângulo sob BAC igual ao sob EDF; desse modo, também o ponto C se ajustará sobre o ponto F, por ser, de novo, a AC igual à DF. Mas, por certo, também o B ajustou-se sobre o E; desse modo, a base BC se ajustará sobre a base EF. Pois se a base BC, tendo, por um lado, o B se ajustado sobre o E, e, por outro lado, o C sobre o F, não se ajustar sobre a EF, duas retas conterão uma área; o que é impossível. Portanto, a base BC ajustar-se-á sobre a EF e será igual a ela; desse modo, também o triângulo ABC todo se ajustará sobre o triângulo DEF todo e será igual a ele, e os ângulos restantes ajustar-se-ão sobre os ângulos restantes e serão iguais a eles, por um lado, o sob ABC ao sob DEF,
e, por outro lado, o sob ACB ao sob DFE. Portanto, caso dois triângulos tenham os dois lados iguais [aos] dois
lados, cada um a cada um, e tenham o ângulo contido pelas retas iguais igual ao ângulo, também terão a base igual à base, e o triângulo será igual ao triângulo, e os ângulos restantes serão iguais aos ângulos restantes, cada um a cada um, sob os quais se estendem os lados iguais; o que era preciso provar.
Caso dois triângulos tenham os dois lados iguais [aos] dois lados, cada um a cada um, e tenham o ângulo contido pelas retas iguais igual ao ângulo, também terão a base igual à base, e o triângulo será igual ao triângulo, e os ângulos restantes serão iguais aos ângulos restantes, cada um a cada um, sob os quais se estendem os lados iguais.
Sejam os dois triângulos ABC, DEF, tendo os dois lados AB, AC iguais aos dois lados DE, DF, cada um a cada
um, por um lado, o AB ao DE, e, por outro lado, o AC ao DF, e o ângulo sob BAC igual ao ângulo sob EDF. Digo que também a base BC é igual à base EF, e o triângulo ABC será igual ao triângulo DEF, e os ângulos restantes serão iguais aos ângulos restantes, cada um a cada um, sob os quais se estendem os lados iguais, por um lado, o sob ABC ao sob o DEF e, por outro lado, o sob ACB ao sob DFE. Pois, o triângulo ABC, sendo ajustado sobre o triângulo DEF, e sendo posto, por um lado, o ponto A sobre o ponto D, e, por outro lado, a reta AB sobre a DE, também o ponto B se ajustará sobre o E, por ser a AB igual à DE; então, tendo se ajustado a AB sobre a DE, também a reta AC se ajustará sobre a DF, por ser o ângulo sob BAC igual ao sob EDF; desse modo, também o ponto C se ajustará sobre o ponto F, por ser, de novo, a AC igual à DF. Mas, por certo, também o B ajustou-se sobre o E; desse modo, a base BC se ajustará sobre a base EF. Pois se a base BC, tendo, por um lado, o B se ajustado sobre o E, e, por outro lado, o C sobre o F, não se ajustar sobre a EF, duas retas conterão uma área; o que é impossível. Portanto, a base BC ajustar-se-á sobre a EF e será igual a ela; desse modo, também o triângulo ABC todo se ajustará sobre o triângulo DEF todo e será igual a ele, e os ângulos restantes ajustar-se-ão sobre os ângulos restantes e serão iguais a eles, por um lado, o sob ABC ao sob DEF,
e, por outro lado, o sob ACB ao sob DFE. Portanto, caso dois triângulos tenham os dois lados iguais [aos] dois
lados, cada um a cada um, e tenham o ângulo contido pelas retas iguais igual ao ângulo, também terão a base igual à base, e o triângulo será igual ao triângulo, e os ângulos restantes serão iguais aos ângulos restantes, cada um a cada um, sob os quais se estendem os lados iguais; o que era preciso provar.Dificuldades
Acredito que a maior dificuldade do texto num geral é a linguagem utilizada nele e a forma como se é exposto as igualdades ou proposições, como por exemplo:
"Sejam os dois triângulos ABC, DEF, tendo os dois lados AB, AC iguais aos dois lados DE, DF, cada um a cada
um, por um lado, o AB ao DE, e, por outro lado, o AC ao DF, e o ângulo sob BAC igual ao ângulo sob EDF."
Poderia ser proposto da seguinte forma:
Sejam dois triângulos ABC e DEF, tendo os lados AB e AC, iguais aos lados DE e DF respectivamente, de forma que o lado AB seja igual ao DE e o lado AC igual ao DF, e também o ângulo sob BÂC igual ao ângulo sob EDF.
Explicação encontrada em livro didático
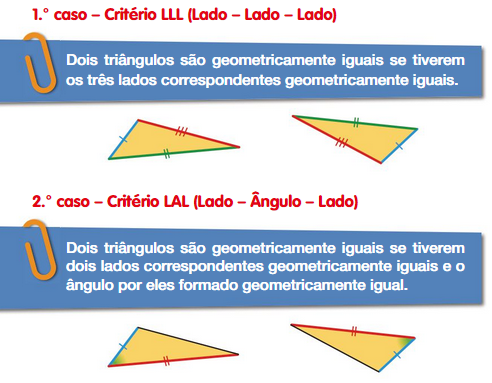
Explicação de Applet
Note no applet acima dois triângulos com dois lados iguais entre eles, ao alterar o valor do ângulo entre estes lados é possível verificar visualmente que eles continuam se mantendo iguais entre si, ao selecionar as caixas para exibir outros valores, é confirmada essa igualdade com valores reais do objeto, como os outros ângulos que se mantem iguais ou lados que não foram dados inicialmente.