Teorema de la Altura
Vamos a desarrollar la demostración del teorema de la altura. Con esta actividad, se pretende desarrollar la competencia matemática del alumno. La competencia matemática implica la capacidad de aplicar el razonamiento matemático y sus herramientas para describir, interpretar y predecir distintos fenómenos en su contexto.
Así también, la competencia matemática requiere de conocimientos sobre los números, las medidas y las estructuras, así como de las operaciones y las representaciones matemáticas, y la comprensión de los términos y conceptos matemáticos.
¿Preparados para la demostración del teorema de la altura? ¡Allá vamos!
El teorema de la altura relaciona la altura de un triángulo rectángulo con las proyecciones de los catetos sobre la hipotenusa, por lo que permite calcular la altura de un triángulo rectángulo conocidas estas proyecciones.
Pero más que aprender esta fórmula, te recomiendo que aprendas el procedimiento de cómo llegar hasta ella, ya que te resultará más fácil también para resolver los problemas.
Vamos a ver cómo es el procedimiento para llegar a esta fórmula.
Para entender el teorema de la altura, primero, debes que entender bien qué son las proyecciones de los catetos sobre la hipotenusa.
Partimos del siguiente triángulo rectángulo, colocado de forma que la hipotenusa queda en la parte de abajo:
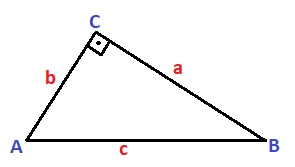Donde:
Por tanto, «n» es la proyección del cateto «b» en la hipotenusa y «m» es la proyección del cateto «a» en la hipotenusa. Ambas proyecciones están separadas por una línea vertical, que corresponde con la altura del triángulo rectángulo.
La altura separa al triángulo en otros dos triángulos rectángulos:
En ambos triángulos, que son semejantes, comparamos su relación entre el cateto menor y el cateto mayor:
En el triángulo de la izquierda, el cateto menor es «n» y el cateto mayor es «h»:
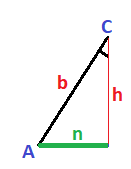En el triángulo de la derecha, el cateto menor es «h» y el cateto mayor es «m» (giro el triángulo 90º hacia la izquierda para que se vea más claro):
Comparamos ambas relaciones y nos queda:
De donde podemos despejar «h», que corresponde a la altura del triángulo rectángulo original.
Para ello, multiplicamos en cruz ambas fracciones, pasando cada denominador multiplicando al miembro contrario:
Operamos en ambos miembros, quedando h² en uno de ellos:
Y finalmente despejamos la altura, pasando el cuadrado como raíz al miembro contrario:
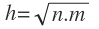Donde llegamos por fin a la fórmula que relaciona la altura con las proyecciones de los catetos en la hipotenusa.
Lo que te debe quedar claro de este teorema es que para llega a su fórmula, comparamos la relación entre el cateto menor y el cateto mayor de los dos triángulos en los que queda dividido por la altura el triángulo original.
Bibliografía:
ekuatio.com
Donde:
- El lado a es el cateto mayor
- El lado b es el cateto menor
- El lado c es la hipotenusa
Por tanto, «n» es la proyección del cateto «b» en la hipotenusa y «m» es la proyección del cateto «a» en la hipotenusa. Ambas proyecciones están separadas por una línea vertical, que corresponde con la altura del triángulo rectángulo.
La altura separa al triángulo en otros dos triángulos rectángulos:
En ambos triángulos, que son semejantes, comparamos su relación entre el cateto menor y el cateto mayor:
En el triángulo de la izquierda, el cateto menor es «n» y el cateto mayor es «h»:
En el triángulo de la derecha, el cateto menor es «h» y el cateto mayor es «m» (giro el triángulo 90º hacia la izquierda para que se vea más claro):
Comparamos ambas relaciones y nos queda:
De donde podemos despejar «h», que corresponde a la altura del triángulo rectángulo original.
Para ello, multiplicamos en cruz ambas fracciones, pasando cada denominador multiplicando al miembro contrario:
Operamos en ambos miembros, quedando h² en uno de ellos:
Y finalmente despejamos la altura, pasando el cuadrado como raíz al miembro contrario:
Donde llegamos por fin a la fórmula que relaciona la altura con las proyecciones de los catetos en la hipotenusa.
Lo que te debe quedar claro de este teorema es que para llega a su fórmula, comparamos la relación entre el cateto menor y el cateto mayor de los dos triángulos en los que queda dividido por la altura el triángulo original.
Bibliografía:
ekuatio.com