Construcción de triángulos y la recta de Euler
Instrucciones
- Realiza las siguientes actividades en las ventana de GeoGebra y contesta a las preguntas que se van haciendo.
- El trabajo que vas haciendo se va actualizando y guardando. No es necesario salvar nada, cuando termines simplemente cierra la ventana.
- Si lo prefieres, puedes realizar los ejercicios en tu ordenador (o en una ventana de GeoGebra online) y abrir tu archivo en la ventana correspondiente al ejercicio.
Actividad 1
Construye un triángulo isósceles con el lado de longitud 7 y longitud de la base 3.
Actividad 2 ¿Cuántos triángulos existen con las longitudes de los lados 4 cm, 5 cm y 8 cm? Dibújalos en la ventana de abajo.
Actividad 3 ¿Cuántos triángulos existen con dos lados de longitudes 5 cm y 7 cm, y el ángulo comprendido de medida 60 grados? Dibújalos en la ventana de abajo.
Actividad 4. La recta de Euler de un triángulo.
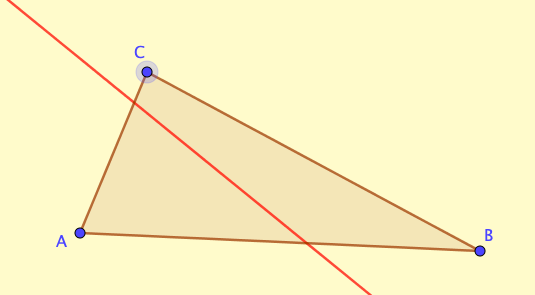
Construye los cuatro puntos notables (baricentro, circuncentro, incentro y ortocentro) del triángulo ABC que aparece en la siguiente ventana y dibuja la recta de Euler, siguiendo los pasos indicados más abajo.
- Construye el baricentro del triángulo ABC (recuerda que el baricentro es la intersección de las tres medianas del triángulo). Utiliza la herramienta "medio o centro"
 .
. - Renombra el punto como "baricentro" y haz que la etiqueta sea visible.
- Esconde las tres medianas.
- Construye el incentro del triángulo ABC (recuerda que el incentro es las intersección de las tres bisectrices del triángulo). Utiliza la herramienta "bisectriz"
 .
. - Renombra el punto como "incentro" y haz que la etiqueta sea visible.
- Esconde las tres bisectrices.
- Construye el circuncentro del triángulo ABC (recuerda que el circuncentro es la intersección de las tres mediatrices del triángulo). Utiliza la herramienta "mediatriz"
 .
. - Renombra el punto como "circuncentro" y haz que la etiqueta sea visible.
- Esconde las tres mediatrices.
- Construye el ortocentro del triángulo ABC (recuerda que el ortocentro es la intersección de las tres alturas del triángulo). Utiliza la herramienta "perpendicular"
 .
. - Renombra el punto como "ortocentro" y haz que la etiqueta sea visible.
- Esconde las tres alturas.
- En este momento deberías de tener visible solamente el triángulo y los cuatro puntos notables del triángulo ABC: el baricentro, el incentro, el circuncentro y el ortocentro. Haz que el triángulo cambie de forma (pinchando en uno de los vértices y arrastrándolo) y observa cómo se mueven los cuatro puntos. ¿Qué observas? ¿Eres capaz de adivinar alguna relación entre ellos?
- La respuesta viene dada por la llamada recta de Euler, que siempre pasa por tres de los cuatro puntos notables del triángulo. ¿Sabrías decir de que puntos se trata? Utiliza el applet de GeoGebra para explorar y buscar una respuesta.
- Una vez que descubras la respuesta, dibuja la recta de Euler.
Pregunta De los cuatro puntos notables de un triángulo, el baricentro, el incentro, el circuncentro y el ortocentro, ¿qué tres de ellos están alineados y contenidos en la recta de Euler?