Google Classroom
GeoGebraClasse GeoGebra
GeoGebra

Cópia de Razões trigonométricas no triângulo retângulo

Auteur :Sandy Dias, Fábio Marson Ferreira

Razões Trigonométricas

Mova os controles deslizantes e b; e observe o que acontece.

Qual segmento de reta representa o cateto oposto ao ângulo Â?

Cochez votre réponse ici
  • A
  • B
  • C
Vérifier ma réponse (3)

Qual segmento de reta representa o cateto adjacente ao ângulo Â?

Cochez votre réponse ici
  • A
  • B
  • C
Vérifier ma réponse (3)

Qual segmento de reta representa a hipotenusa?

Cochez votre réponse ici
  • A
  • B
  • C
Vérifier ma réponse (3)
Por meio dos controles deslizantes e b, você pode variar o valor do ângulo  e do cateto b. Verifique que, ao se modificar o comprimento de b mantendo-se o valor do referido ângulo inalterado, as razões trigonométricas não se alteram. Entretanto, ao se variar o valor do ângulo, mantendo-se inalterado o comprimento do lado b, as razões variam, indicando haver uma relação entre estas e o valor do ângulo.

Por que você acha que as razões não se alteram quando o controle deslizante de b é movido?

Vérifier ma réponse

Por que as razões variam quando o controle deslizante referente ao ângulo  é movido?

Vérifier ma réponse
A partir do que foi trabalhado, podemos agora conhecer um pouco melhor sobre o que são as razões trigonométricas, estas estão relacionadas com os ângulos de um triângulo retângulo e as principais razões são: o seno, o cosseno e a tangente. As relações trigonométricas são resultado da divisão entre as medidas de dois lados de um triângulo retângulo, e por isso também são chamadas de razões. Observamos na construção acima que a hipotenusa é o lado oposto ao ângulo reto e o maior lado do triângulo. Já os catetos são os lados adjacentes e que formam o ângulo de 90°. Sendo assim, podemos dizer que as razões trigonométricas no triângulo retângulo são:

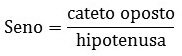
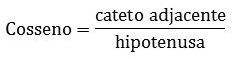
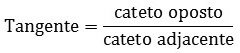
Utilizando a construção acima, responda: (Cefet – PR/ modificada) A rua Tenório Quadros (representada pelo segmento c) e a avenida Teófilo Silva (representada pelo segmento b) , ambas retilíneas,  cruzam-se conforme um ângulo de 40º. O posto de gasolina Estrela do Sul (representada pelo vértice C ) encontra-se na avenida Teófilo Silva a 10 m do citado cruzamento. Sabendo que o percurso do posto Estrela do Sul até a rua tenório quadros forma um ângulo de 90° no ponto de encontro do posto com a rua Teófilo Silva, determine, o valor do Seno, Cosseno e Tangente do ângulo formado entre as ruas Tenório Quadros e Teófilo Silva.

Vérifier ma réponse

Nouvelles ressources

Découvrir des ressources

Découvrir des Thèmes