Convergent/divergent Test of a Sequence
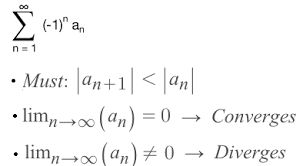
The convergence/divergence test is a method used to determine whether a given sequence converges or diverges. It helps analyze the behavior of the terms in a sequence and provides insights into its long-term behavior.
There are various convergence/divergence tests available, each with its own conditions and applicability. Let's discuss some commonly used tests:
1. Limit Test:
The limit test states that if the limit of a sequence, as n approaches infinity, exists and is finite, then the sequence converges. Mathematically, if lim(n→∞) an = L (where "an" represents the terms of the sequence), and L is a finite number, then the sequence converges. If the limit does not exist or is infinite, the sequence diverges.
2. Comparison Test:
The comparison test involves comparing a given sequence with another known sequence to determine convergence or divergence. Suppose we have two sequences, "an" and "bn," and we know that bn is convergent. If an ≤ bn for all n, then if bn converges, an also converges. Similarly, if bn diverges, an also diverges.
3. Ratio Test:
The ratio test examines the ratio of consecutive terms in a sequence. If lim(n→∞) |an+1/an| = L < 1, where "an" represents the terms of the sequence, then the sequence converges. If L > 1 or if the limit does not exist, the sequence diverges.
4. Root Test:
The root test analyzes the n-th root of the absolute value of each term in a sequence. If lim(n→∞) |an|^(1/n) = L < 1, where "an" represents the terms of the sequence, then the sequence converges. If L > 1 or if the limit does not exist, the sequence diverges.
5. Integral Test:
The integral test relates the convergence of a sequence to the convergence of an associated function. Consider a sequence "an" and the corresponding function f(x). If f(x) is continuous, positive, and decreasing for x ≥ 1, and the integral of f(x) from 1 to infinity converges, then the sequence "an" also converges. If the integral diverges, then the sequence diverges.
It's important to note that these tests provide guidelines and conditions for convergence or divergence, but they may not always yield conclusive results for every sequence. Sometimes a sequence may not satisfy the conditions of a specific test, requiring the use of other techniques or approaches for analysis.
By applying these mathematical tests, we can assess the convergence or divergence of a sequence and gain insights into its long-term behavior.
Examples:
Here are examples illustrating the convergence/divergence tests using mathematical formulas:
1. Limit Test:
Consider the sequence an = 1/n. To determine its convergence, we evaluate the limit as n approaches infinity: lim(n→∞) (1/n) = 0. Since the limit is finite (0), the sequence converges.
2. Comparison Test:
Let's consider the sequence an = (3n2 + 2n)/(4n2 + n + 1). We compare it with the sequence bn = (3n2)/(4n2) = 3/4. Since 0 ≤ an ≤ bn for all n, and bn = 3/4 is convergent, we conclude that the sequence an also converges.
3. Ratio Test:
Take the sequence an = (n2)/(2n). We apply the ratio test: lim(n→∞) |(n+1)2/(2(n+1) )/ |(n2)/(2n)| = 1/2. Since the limit is less than 1, the sequence converges.
4. Root Test:
Consider the sequence an = (3^n)/(n!). We apply the root test: lim(n→∞) |(3n)(1/n)/ (n!)(1/n)= 3/e. Since the limit is less than 1, the sequence converges.
5. Integral Test:
Let's examine the sequence an = 1/n. We associate it with the function f(x) = 1/x. The function is continuous, positive, and decreasing for x ≥ 1. By evaluating the integral of f(x) from 1 to infinity, we have ∫(1 to ∞) 1/x dx = ln(x) |(1 to ∞) = ln(∞) - ln(1) = ∞. Since the integral diverges, the sequence an also diverges.
These examples illustrate the application of convergence/divergence tests to different sequences. It's important to carefully analyze the conditions of each test and apply them appropriately to draw conclusions about the convergence or divergence of a given sequence.