Bernoulli's Inequality Theorem
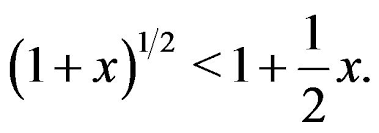
In mathematics, Bernoulli's inequality (named after Jacob Bernoulli) is an inequality that approximates exponentiations of 1 + x. It is often employed in real analysis. It has several useful variants.
Bernoulli’s inequality theorem states:
Theorem 1. For all real number x > −1 and real number r > 1, the following inequality holds
(1 + x)r ≥ 1 + rx. The equality holds if and only if x = 0.
The inequality sign changes when 0 < r < 1, that is (1 + x) r ≤ 1 + rx. If we let x + 1 → x, the inequality can be restated as:
Theorem 2. For all x > 0 and r > 1, x r ≥ rx + 1 − r. The equality holds if and only if x = 1.
Inequality (2) is used more often than its original form. Let r = a b with a > b > 0 and
x → x b , we have Theorem 3. Let a, b ∈ R + and a > b. Then for all
x > 0, x a ≥ a b x b + 1 − a b .
This inequality looks more appealing than the other two because it allows us to compare x with the difference between the two powers. One of the strengths of this inequality is that it can be applied for inequalities with irrational powers and non-homogeneous inequalities.
Examples
Bernoulli's Inequality is a fundamental inequality in mathematics that relates the exponential function to the power function. It states that for any real number 'x' greater than -1 and any real number 'r' greater than or equal to 0:
(1 + x)r ≥ 1 + r * x
where:
- x is a real number greater than -1.
- r is a real number greater than or equal to 0.
This inequality tells us that raising a number greater than -1 to a positive power will always result in a value greater than or equal to 1 + r * x.
**Examples:**
1. x = 0.5, r = 2:
(1 + 0.5)2 ≥ 1 + 2 * 0.5
1.52 ≥ 1 + 1
2.25 ≥ 2
Here, the inequality holds true, as 2.25 is indeed greater than 2.
2. x = 0.2, r = 4:
(1 + 0.2)4 ≥ 1 + 4 * 0.2
1.24 ≥ 1 + 0.8
1.7490064 ≥ 1.8
Again, the inequality is satisfied since 1.7490064 is greater than 1.8.
3. x = -0.1, r = 3
(1 - 0.1)3 ≥ 1 + 3 * (-0.1)
0.93 ≥ 1 - 0.3
0.729 ≥ 0.7
Even with a negative value of 'x', the inequality remains true, as 0.729 is greater than 0.7.
Bernoulli's Inequality finds applications in various fields of mathematics and serves as a useful tool for proving more complex inequalities and theorems. It is an essential concept in the study of mathematical analysis and plays a role in various branches of mathematics, including calculus and number theory.