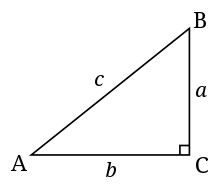
L'utilité du théorème de Pythagore :

Pythagore fit connaître une équerre dont la découverte ne devait rien aux techniques artisanales, et là où les constructeurs d'équerres, à force de travail, ont grand mal à obtenir une forme exacte, les méthodes de calcul tirées de son enseignement permettent de se tirer d'embarras. Voici le fait : si l'on prend trois règles dont l'une ait trois pieds de long, la seconde quatre et la troisième cinq, et si on les dispose de manière que leurs extrémités soient en contact, elles figureront un triangle qui représentera une équerre correcte. D'autre part, si l'on construit un carré sur la longueur de chacune de ces règles, celui dont le côté sera de trois pieds aura neuf pieds de surface ; celui dont le côté sera de quatre aura seize pieds ; celui dont le côté sera de cinq en aura vingt-cinq. Ainsi le nombre total de pieds représentant la surface des deux carrés de trois et quatre pieds de côté est exactement égal à celui que donne à lui seul le carré construit sur la base de cinq pieds

À cette découverte, Pythagore, persuadé qu'il devait aux Muses l'inspiration de sa trouvaille, en témoignage de sa vive reconnaissance leur immola, dit-on, des victimes. Cette méthode, souvent utile pour bien des mesures, est commode également pour la construction des escaliers dans les bâtiments : elle permet de donner aux marches des positions convenables. En effet, si l'on divise en trois parties la hauteur de l'étage, du plafond au niveau du sol, la pente des limons, dans l'escalier, en aura exactement cinq de long ; par conséquent, en prenant des divisions égales aux trois qui séparent le plafond et le niveau du sol, on devra ménager un retrait de quatre divisions à partir de la verticale, et placer à cet endroit les semelles inférieures des limons. De cette façon, les marches mêmes de l'escalier se trouveront elles aussi convenablement disposées.