Isosceles Triangle Theorem and its Converse
Isosceles Triangle Theorem and its Converse
In an isosceles triangle, two sides (legs) of the triangle are congruent. In the isosceles triangle below, sides AB and AC are the congruent legs. BC is the base. Angle A is the vertex angle (opposite the base) and Angles B and C are the base angles.
Move the vertices of the isosceles triangle, and identify the relationship between the sides and angles of the isosceles triangle.
1. What do you notice about the base angles (Angle B and Angle C) of the isosceles triangle ABC, as you move the vertices of the triangle.
Isosceles Triangle Theorem: If two sides of a triangle are CONGRUENT, the angles opposite are CONGRUENT.
or
BASE angles of an isosceles triangle are CONGRUENT
The converse is also TRUE.
Converse of the Isosceles Triangle Theorem: If two angles of a triangle are CONGRUENT, the sides opposite are CONGRUENT.
2. In triangle ABC, side AB is congruent to side AC.
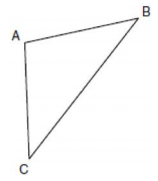
Make another congruent statement about triangle ABC.
3. In triangle SAM, angle S is congruent to angle A.
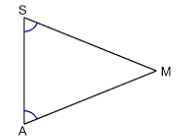
Make another congruent statement about triangle SAM.