CAS Functions 4 Gauß-Algorithm
nn = Matrix-Zeilen (Matrix-Dimension)
Zeilen-Spalten-Tausch (row/col exchange)
Zeilen-Spalten-Operationen (row/col op)
Gauß-Schritt, Vorwärts-Substitution (gauss-step substitution to upper triangular matrix)
Elementarmatrizen für Spalte jj (benötigt E(zle,spl,fzs,nn))
Elementarmatrizen Vorwärts-Substitution, Liste für Spalte ss
Elementarmatrizen zur Rücksubstitution, Liste für Spalte ss (benötigt E(zle,spl,fzs,nn))
Vorwärts-Substitution Spalte zz (2..n) von MM == Null
Diagonale 1en für GaussSubst
Rücksubstitution zur Einheitsmatrix,
Spalte zz (n..2) von MM == Nul
LR-Zerlegung auf einem Matrixfeld - i,j nicht anderweitig verwenden!
Spalte kk (1...n-1)
Sei LR=LRdecomp(A,n-1) die abgeschlossene LR-Zerlegung von A die L,R enthält
L,R herausziehen (getL, getR)
T(zz,ss,nn):=Sequence(Element(Identity(nn), If(kk<>zz &&
kk<>ss,kk, If(kk==zz,Max(zz,ss),Min(zz,ss)))),kk,1,nn)
Zeilen-Spalten-Operationen (row/col op)
E(zle,spl,fzs,nn):=Sequence(Sequence(Element(Identity(nn), zz,ss)-1*(zle==spl && zle==zz &&spl==ss)*1+If(zz==zle && ss==spl,fzs,0),ss,1,nn),zz,1,nn)
Gauß-Schritt, Vorwärts-Substitution (gauss-step substitution to upper triangular matrix)
Elementarmatrizen für Spalte jj (benötigt E(zle,spl,fzs,nn))
LE(AA,jj):=Sequence(E(k,jj,-Element(AA,k,jj)/Element(AA,jj,jj)),k,n,jj+1)
Elementarmatrizen Vorwärts-Substitution, Liste für Spalte ss
LE(AA,ss):= Sequence(Sequence(If(j==ss && k>ss, If(k==ss,1,-1) Element(AA,k,ss)/Element(AA,ss,ss),(j==k)*1), j ,1,Length(AA)),k,1,Length(AA))
Elementarmatrizen zur Rücksubstitution, Liste für Spalte ss (benötigt E(zle,spl,fzs,nn))
RE(AA, jj):=(Sequence(E(k,jj,-Element(AA,k,jj),Length(AA)),k,1,jj-1)) ;
Vorwärts-Substitution Spalte zz (2..n) von MM == Null
GaussTriag(MM,zz):=Sequence( If(kk>zz ,Element(MM, kk) - Element(MM,kk,zz)/Element(MM,zz,zz) Element(MM,zz),Element(MM,kk)) ,kk,1,Length(MM))
Diagonale 1en für GaussSubst
GaussDiag(MM):=Sequence(If(Element(MM,kk,kk) <> 0, Element(MM,kk)/Element(MM,kk,kk),Element(MM,kk)),kk,1,Length(MM) )
Rücksubstitution zur Einheitsmatrix,
Spalte zz (n..2) von MM == Nul
GaussSubst(MM,zz):=Sequence(If(kk < zz,Element(MM,kk)-Element(MM,kk,zz) Element(MM,zz),Element(MM,kk)),kk,1,Length(MM));
LR-Zerlegung auf einem Matrixfeld - i,j nicht anderweitig verwenden!
Spalte kk (1...n-1)
LRdecomp(AA,kk):=Join(Take(AA,1,kk),Sequence(Sequence(If(i < kk,Element(AA, j,i),If(i==kk,Element(AA,j,kk)/Element(AA,kk,kk),Element(AA, j,i)-Element(AA,j,kk) (Element(AA,kk,i)/Element(AA,kk,kk)))), i,1,Length(AA)),j,kk+1,Length(AA)));
Sei LR=LRdecomp(A,n-1) die abgeschlossene LR-Zerlegung von A die L,R enthält
L,R herausziehen (getL, getR)
R:=Sequence(Take(Join(Sequence(0,i,1,j),Take(Element(LR,j),j,Length(LR))),2,Length(LR) + 1),j,1,Length(LR))
L:=Join(Take(Identity(Length(LR)),1,1),Sequence(Join(Take(Element(LR,j),1,j- 1), Take(Element(Identity(Length(LR)),j),j,Length(LR))),j,2,Length(LR)))
---
Don't forget to close function input with [keep Input]
CAS-User-Functions.ggb
IterationList
Die Algorithmen der Matrizenrechnung lassen sich rekursiv darstellen,
sei z.B. LX(Aj-1 , j ) eine Elementarmatrizenfolge, um in Aj-1 eine Spalte Nullen unter dem Diagonallement j zu erzeugen. Um eine obere Dreiecksmatrix zu erzeugen wären j=1..n-1 Spalten zu bearbeiten:
Anstatt für jeden Schritt eine CAS-Zeile anzulegen
A1 = LX(A0,1) A0
A2 = LX(A1,2) A1
A3 = LX(A2,3) A2
kann
Iteration( «Expression», «Variables», «Start Values», «Count» )
IterationList({Element(a,1) + 1, LX(Element(a,2), Element(a,1) + 1) * Element(a,2)},a,{{0, A0}},3)
diese Schritte zusammenfassen, wenn für Expression und Laufvariable a eine spezielle Listenform gewählt wird:
«Variables», «Start Values» == a , {{0, A0}}
j == Element(a,1) Element(a,2) == Aj-1
Iteration() statt IterationList() stellt nur den letzten Iterations-Schritt dar!
Beispielsweise angewendet auf die LR-Zerlegung ohne Pivotsuche
(12) A:= {{2,1,-3,4},{4,1,-4,9},{-2,1,0,-5},{2,2,-5,1}}
(13) IterationList({Element(a,1)+1,LRdecomp(Element(a, 2),Element(a, 1)+1) }, a, {{0, A}},3)
Auskopplung von L, R
(14) iR:=getR(Element($13,4,2))
(15) iL:=getL(Element($13,4,2))
(18)-(26) LR-Zerlegung mit Pivotsuche
nach jedem Schritt muß die Tauschmatrix für die Pivotzeile ermittelt werden.
Wenn man die Tauschmatrizen erstmal ermittelt hat und in eine Liste stellt
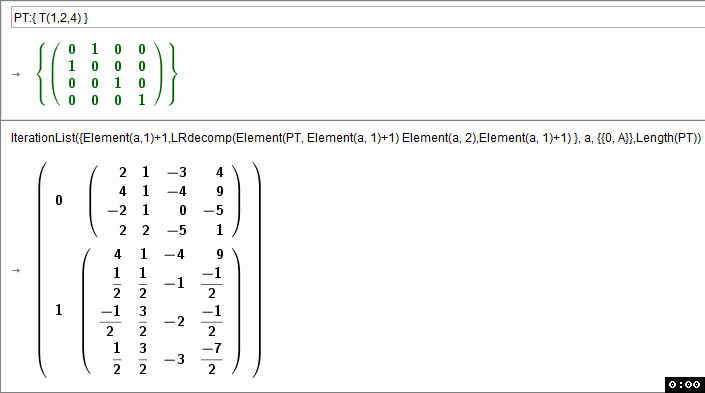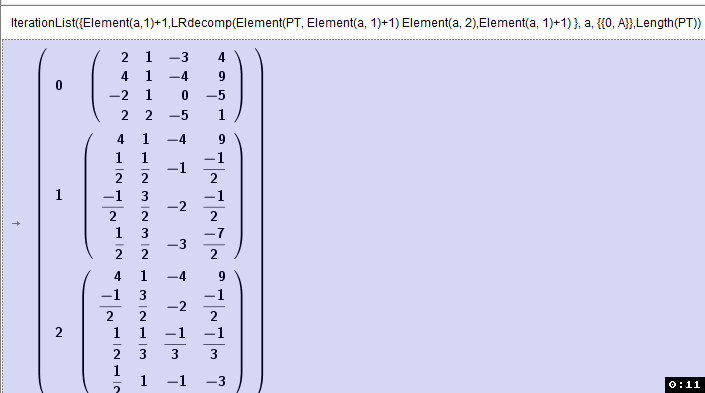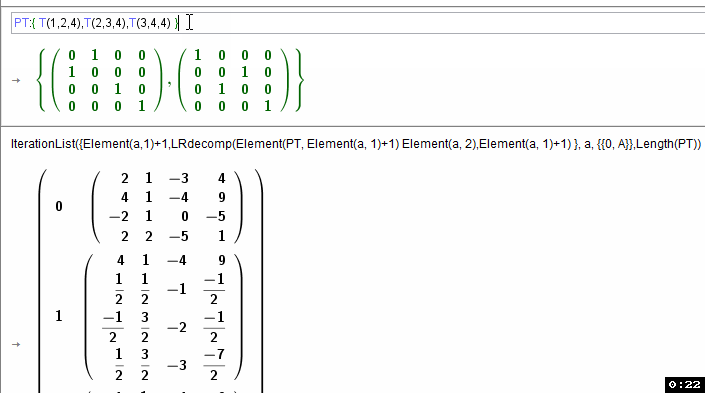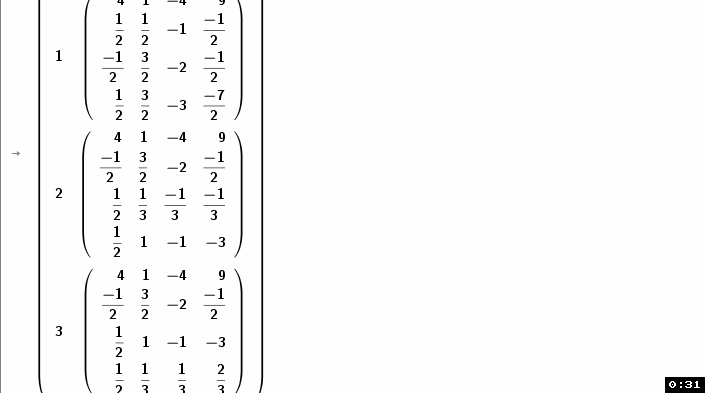
PT:{ T(1,2,4),T(2,3,4),T(3,4,4) }
dann kann rekrusiv mit
IterationList({Element(a,1)+1,LRdecomp(Element(PT, Element(a, 1)+1) Element(a, 2),Element(a, 1)+1) }, a, {{0, A}},Length(PT))
iteriert werden...
stepwise column pivot recursiv iteration
