Relação de Euler
Introdução
Nos estudos dos poliedros convexos, é interessante podermos calcular o número de vértices, faces e arestas. Porém não é interessante contar manualmente ou realizar o desenho do poliedro que estamos analisando, pois muitas vezes exige habilidade de desenho que não dispomos e é muito trabalho. Vamos trabalhar com um teorema desenvolvido por Euler, que serve como uma relação dos poliedros e facilitará nosso trabalho.
Mas antes, vamos relembrar os conceitos de vértice, aresta e face.
Agora vamos aprender como é formada a relação de Euler e veremos um exemplo:

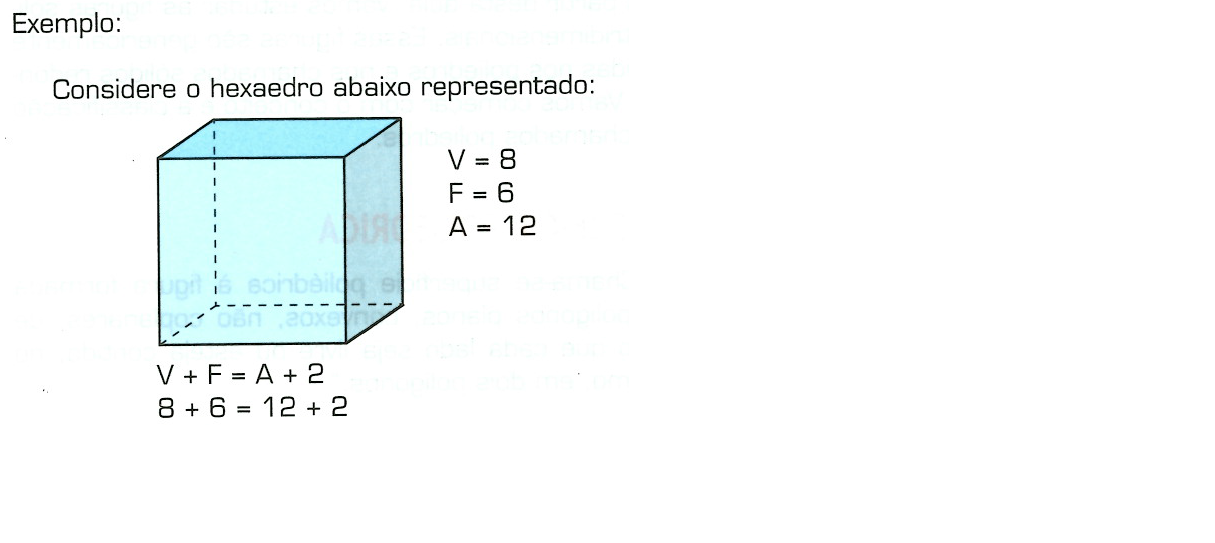
Agora, fazendo estes cálculos para alguns dos poliedros mais notáveis, desenvolvemos a seguinte tabela:
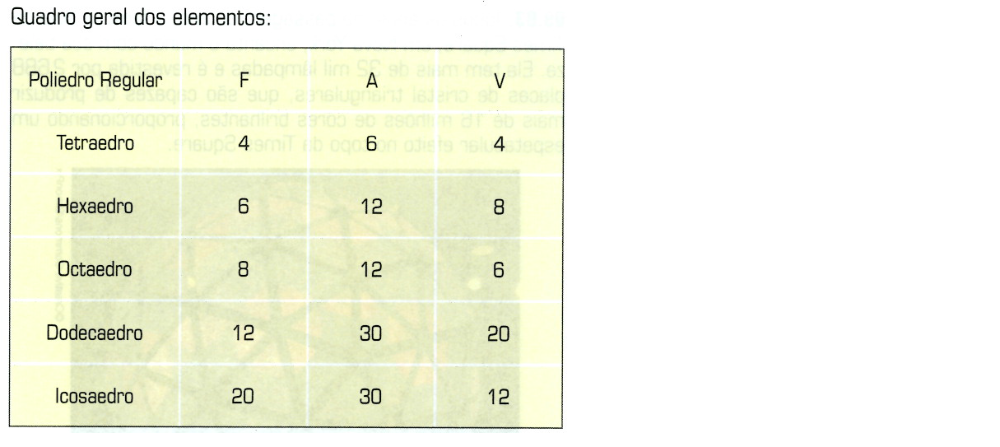
Sobre os seus conhecimentos adquiridos anteriormente, responda:
1) Um turista ecológico encontrou, em uma de suas viagens, um cristal de rocha no formato de um poliedro convexo de 60 faces triangulares. Qual o número de arestas e vértices desse cristal?
2) Faça uma breve pesquisa, e lista abaixo quais são os poliedros de Platão.