Euler's reaction
First reaction
Euler's reaction is rather sceptic:
. . . Thus you see, most noble Sir, how this type of solution
bears little relationship to mathematics, and I do not understand why you
expect a mathematician to produce it, rather than anyone else, for the solution
is based on reason alone, and its discovery does not depend on any
mathematical principle. Because of this, I do not know why even
questions which bear so little relationship to mathematics are solved more
quickly by mathematicians than by others.
trivial but intriguing...
Although Euler thought it to be rather a trivial problem, it keeps intriguing him and he writes to Giovanni Marinoni, an Italian mathematician and engineer:
"This question is so banal, but seemed to me worthy of attention in that [neither] geometry, nor algebra,
nor even the art of counting was sufficient to solve it."
Euler believes this problem was related to a topic that Leibniz had once discussed and longed to work with, something Leibniz referred to as geometria situs, or geometry of position. And how does a mathematician deal with such kind of problems? He makes a generalization of it and establishes a model, that will turn out to be the start of graphing theory and of topology.
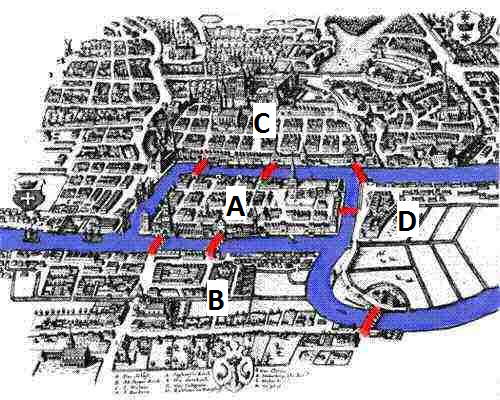
How do you start a work around?
As mathematician Euler knows you'd better start by generalizing a problem. So you don't speak anymore about a town, islands and bridges using their proper names. Instead you say that the river devides the city in four parts A, B, C en D, connected by 7 links. If you cross a bridge, going from part A to B, you just note it as AB. If you go from A to B and cross a second bridge to C and a third to D, you simply note it as ABCD. Euler immediately sees that you need one letter more than the number of bridges to cross. In other words: to cross seven bridges you need 8 letters. Euler is the first one to examine a similar problem systematically.
More than 100 years later, James Joseph Sylvester introduces in 1878 a graphical representation of such systems. And so we end up with graphs: a representation with points, connected by lines.
Now the problem of the bridges is turned into the question 'what are the properties of such graphs ?'