ANÁLISIS DE LOS PARÁMETROS DE LA FUNCIÓN LINEAL y=mx+b
CASO 1. Variación del parámetro “m” en la función lineal y = mx +b. donde m>0 ó m<0 y con b=0
Realiza lo que se indica en cada pregunta y expresa con tus palabras todo lo que observas y concluyes de ello
¿Qué sucede con la gráfica cuando el parámetro “m” de la función toma valores positivos?
¿Qué pasa cuando el parámetro “m” toma valores negativos?
Considerando que en las situaciones anteriores el valor modificado fue el correspondiente al parámetro "m" y habiendo observado el comportamiento de la grafica A que conclusión llegas...
CASO 2. Variación del parámetro “b” en la función lineal y = mx +b. donde m=0 con b>0, b<0, b=0
¿Qué pasa con la gráfica cuando el parámetro "m" = 0 y b es un número positivo?
Y cuando el parámetro "m" = 0 y "b" es un número negativo, ¿Qué comportamiento toma la gráfica?
¿Qué ocurre cuando m = 0 y b = 0?
Caso 3. Variación del parámetro “b” en la función lineal y = mx +b. donde m= 1 con b>0, ó <0
¿ Y cuándo es negativo el valor de “b” que sucede?
¿Y qué ocurre con la gráfica cuando “b” es positivo?
¿ Cómo se relaciona el cambio de valor al parámetro b y el corte de la recta en el eje de las ordenadas (eje y)?
A continuación, tienen algunos enunciados para completar. Elige cuál de las opciones completa o responde cada uno.
La pendiente de la recta indica:
La ordenada al origen de una recta indica:
Observa la información de la siguiente tabla y partir de los datos ofrecidos determina los faltantes

Anota aquí tus respuestas a sobre la tabla anterior
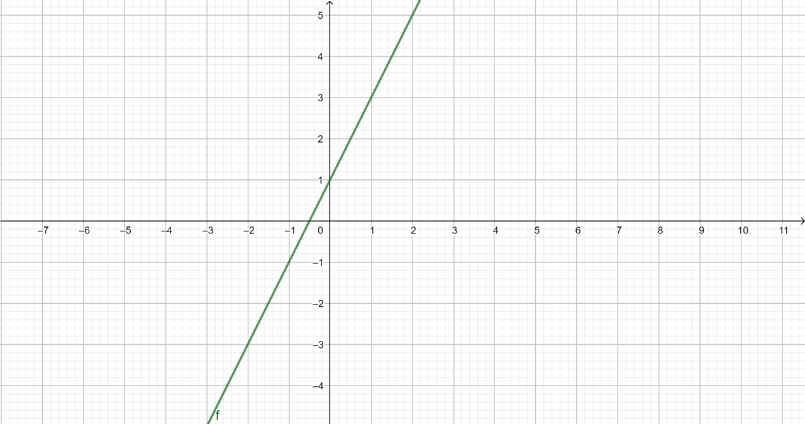
Ahora ya habiendo analizado los parámetros de la función lineal y=mx+b puedes determinar una función a partir de su grafica para ello observa la gráfica y determina cada uno de los parámetros involucrados y con ello establece el la expresión algebraica
Escribe la expresión algebraica que representa a la función de la gráfica anterior.
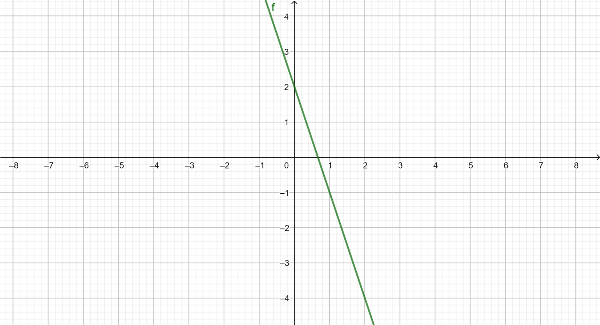
Observa la siguiente recta y contesta
Escribe la expresión algebraica correspondiente la función de la grafica anterior
Por ultimo grafica la siguiente función lineal y=3x-1
Dada la función y = 2x – 4, señala todas las frases que sean verdaderas.
Si la pendiente de una función lineal es positiva, la función es:
Si la pendiente de una función es cero, la función es:
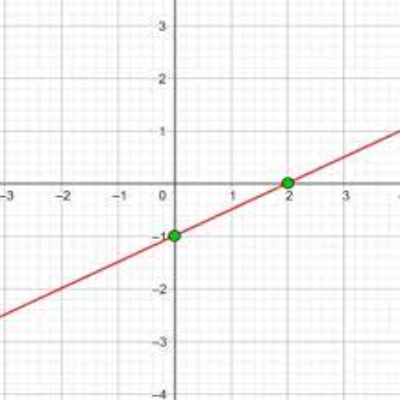
La función representada en la imagen: