Clases de Matemáticas y Física
Introducción y consignas
DESCRIPCIÓN: El siguiente material es una guía de ejercicios, basados en principios simples de las matemáticas; pero cuyas aplicaciones prácticas tienen un gran impacto.
ORGANIZACIÓN DEL MATERIAL: La mayoría de las secciones dentro de esta guía, están introducidas por una gran duda del pasado, el trabajo de alguna o algún pensador del pasado, la aplicación de su teoría para responder dicha duda, y otros ejemplos de aplicación.
INTRODUCCIÓN: Es muy importante para el desarrollo de esta actividad, realizar anotaciones, dudas, observaciones y conclusiones propias para los fenómenos observados, pues nos permiten ejercitar partes esenciales del método científico. Realizar un registro escrito, fotográfico o material, de los procesos de una investigación, nos permiten recaudar fuentes de información que facilitan recorrer nuestros propios pasos, evitar pasarnos por alto datos importantes, y compartir con otras personas nuestros descubrimientos.
Recordá, que ningún conocimiento científico surge de manera espontanea, independiente de conocimientos previos o en soledad. La mayoría de las grandes mentes de nuestro tiempo y del pasado, han empleado conocimientos y dudas de previos, y se han acercado a otras personas para pedir consejo o debatir ideas.
Ciertamente, las ciencias, son una forma de producción humana, como las artes o la cultura. No se hacen en soledad, y sólo tienen valor cuando se pueden compartir con otras personas. Es por esto que poder confeccionar registros escritos claros de nuestros trabajos y observaciones, no solo en benéfico para nuestras prácticas científicas, sino para nuestras personas en un ámbito de personas.
OBSERVACIONES: No es necesario realizar todas las actividades propuestas. Esto es un extra, y queda a su criterio, hasta donde prefiere realizar. No se esfuerce de más, pues no es saludable, y no es una buena práctica científica trabajar hasta el cansancio. Aprender a identificar tiempos de trabajo cómodos, saber de nuestro propio cuerpo y su cansancio, es esencial para ser un o una gran persona de ciencia.
¿Cuál es la forma de la Tierra?
Esta pregunta, ha circulado por la mente de las personas durante mucho tiempo. Tal vez hace 12.000 años, al inicio de las civilizaciones antiguas, o tal vez incluso antes.
Conocer la forma de la Tierra, tiene una gran cantidad de aplicaciones, pero para un habitante normal de la superficie terrestre, probablemente sea simplemente un dato que satisface su curiosidad.
Si bien, hoy podemos reconocer que la Tierra es esférica (y no redonda, porque redondos son los círculos, figuras geométricas en dos dimensiones y no en tres), se entiende que tampoco es correcto. Es aceptado actualmente el término Geoide, que significa "Con forma de Tierra" (Geo: Tierra, Oide: Similar a). Debido a que las irregularidades como montañas o ríos, le dan una forma diferente de esférica a la superficie de esta, y porque, los polos se encuentran más cerca entre si, que los puntos extremos sobre el ecuador.
Esfera
Geoide
Una de las primeras personas en determinar que la Tierra no es plana como se creía anteriormente fué Surya Siddhanta en el 2000 A.C., incluso se han encontrado escritos Egipcios del 2500 A.C. que defienden una idea similar.
Los pensadores Árabes no solo son los creadores del Álgebra (una de las disciplinas fundamentales de las matemáticas), sino que también reintroducieron a Europa en el 1300 D.C. los textos de autores griegos que habían sido olvidados luego de que el Imperio Romano ocupase sus tierras. Pero las poblaciones Arábigas que habían interactuado con los griegos en el pasado, conocían de sus trabajos y podían traducir sus textos. Así es como se recuperan los desarrollos de autores como Eratóstenes, quien no solo probó la curvatura de la tierra, sino que también su tamaño.

Eratóstenes y la curvatura de la Tierra (235 A.C.)
Para la época, era conocido que una fuente de luz que impacta contra un objeto, proyecta más allá de él una sombra. Es así, como en los días calurosos, podemos evitar los rayos del sol escondiéndonos debajo de la sombra de los árboles.
Eratóstenes propuso, que si la Tierra fuese plana, al colocar dos columnas a cierta distancia entre ellas perpendiculares a la Tierra, cuando el sol pasa justo por encima de una, proyectando una sombra mínima sobre está, debería proyectar una sombra mínima sobre la otra.
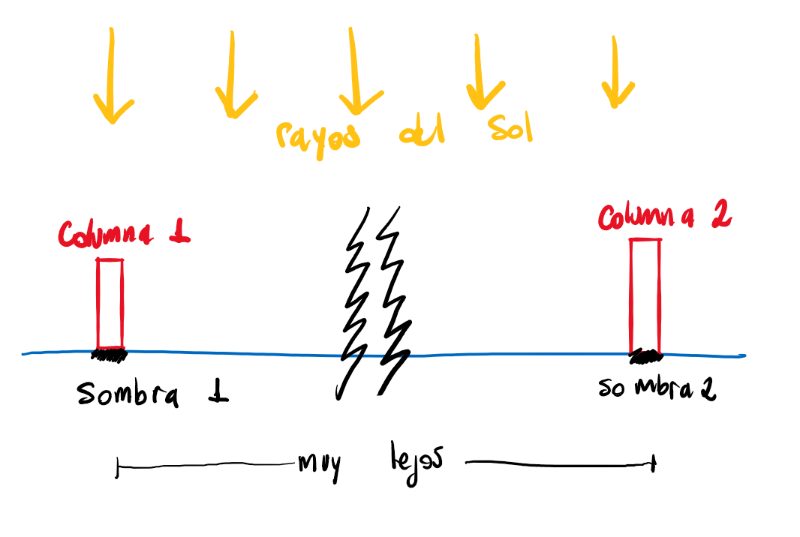
La propuesta del experimento consistía en suponer, que:
- Todos los rayos de luz que llegan a la tierra son paralelos entre ellos.
- A una misma altura sobre el nivel del mar, la sombra proyectada sobre una columna, es la misma sobre otra al mismo tiempo.
Finalmente, llegaron los resultados a dicho experimento:
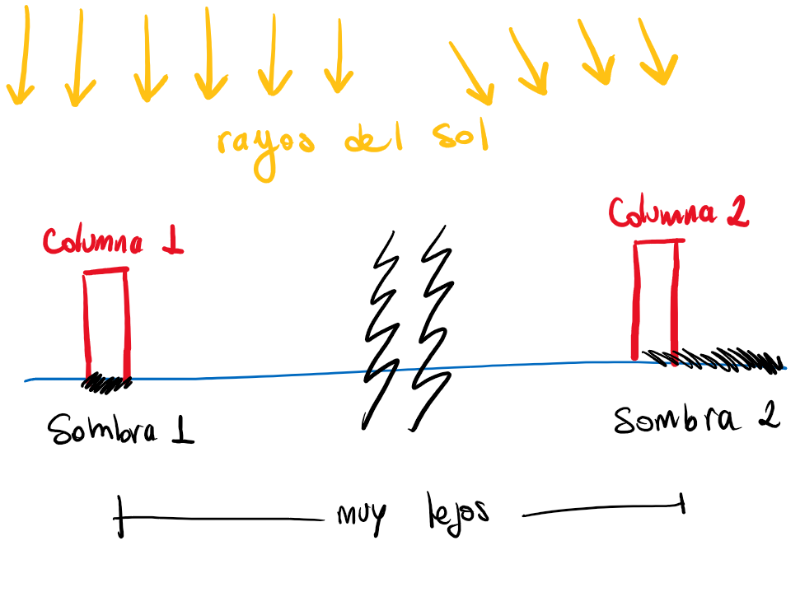
Los rayos, en ambos lugares, a pesar de ser la misma hora, arriban de maneras diferentes. De manera que, si todos los rayos del sol, llegan de manera paralela, aquello que se encuentra inclinado, es la tierra.
Si se realiza el mismo experimento, a diferentes distancias, se pueden observar diferentes medidas de sombra.
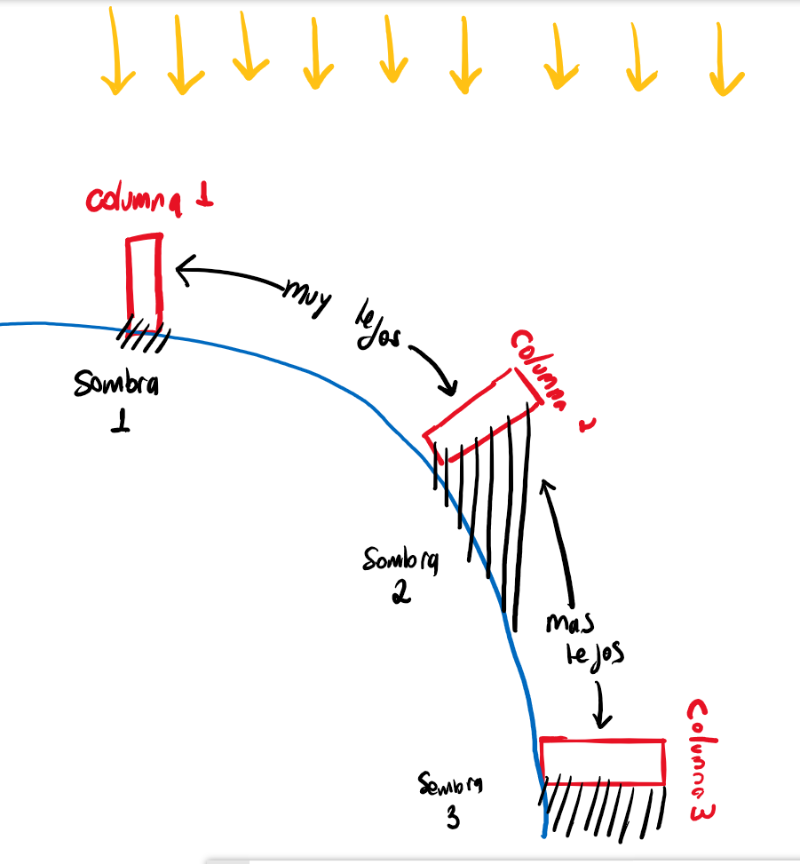
Finalmente, a partir de este modelo, y la realización de múltiples otros experimentos en la época, hasta incluso el siglo XV D.C., fué aceptado que la Tierra es cercana a ser una esfera.

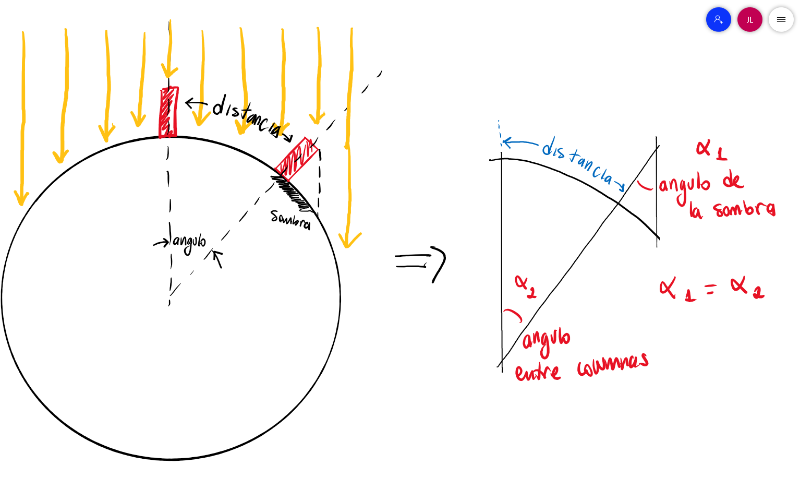
Debido a que el ángulo formado por la sombra, es el mismo que aquel formado entre ambas columnas con respecto al centro de la Tierra, y la distancia entre cada columna, fué posible para Eratóstenes, calcular las dimensiones generales del Planeta.
Así es como se obtuvo que el radio del planeta es 6370 kilómetros, y su circunferencia de 40.000 kilómetros.
Una de las aplicaciones de este conocimiento más importantes, fué para saber el tamaño de la Luna.
Fué Aristarco quien en 240 A.C., a partir del conocimiento sobre el tamaño de la Tierra, estimó el tamaño de la Luna.
Usando su conocimiento sobre la forma en que los objetos proyectan su sombra, observó la sombra que se forma sobre la Luna, cuando el Sol la ilumina con la Tierra en medio.
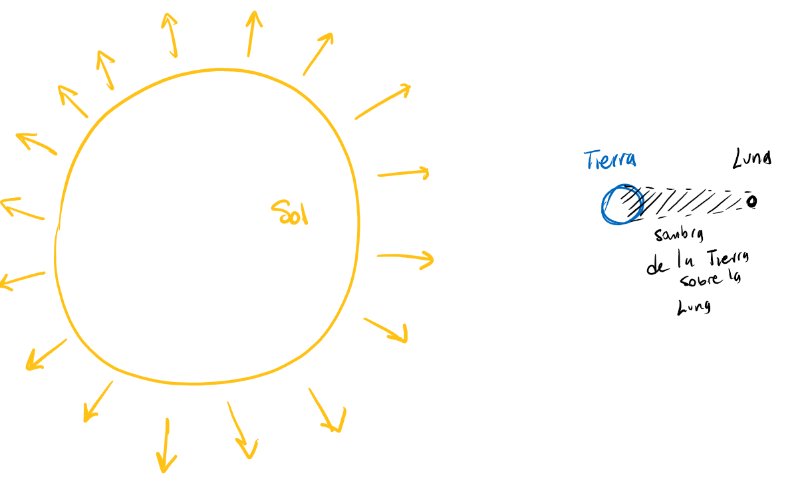
Resultando que el radio de la Luna es de 1820 kilómetros.
Saber el tamaño de la Luna permitió saber a qué distancia se encuentra.
A partir de un principio matemático denominado Teorema de Tales, en honor a Tales de Mileto, es posible estimar la distancia a la Luna, a partir de una regla y una moneda.
El Teorema de Tales, permite calcular la longitud de segmentos desconocidos a partir de atravesar rectas por 3 o más paralelas.
De manera que una forma derivada del Teorema propone:
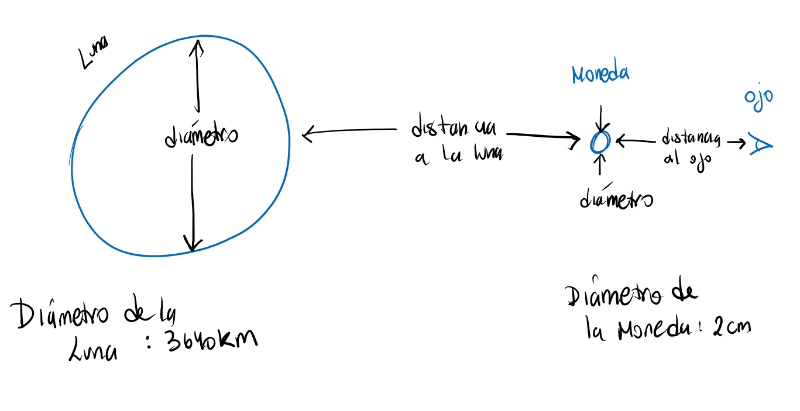
1. Colocar una moneda de diámetro conocido, en un vidrio o ventana que dá al cielo.
2. Esperar que sea de noche, y que la Luna sea visible.
3. Posicionar el ojo de una manera que la moneda tape la Luna.
4. Medir la distancia a la que se encuentra el ojo de la moneda.
5. Resolver la siguiente ecuación:
La única incógnita o dato desconocido el la distancia entre la moneda y la luna.
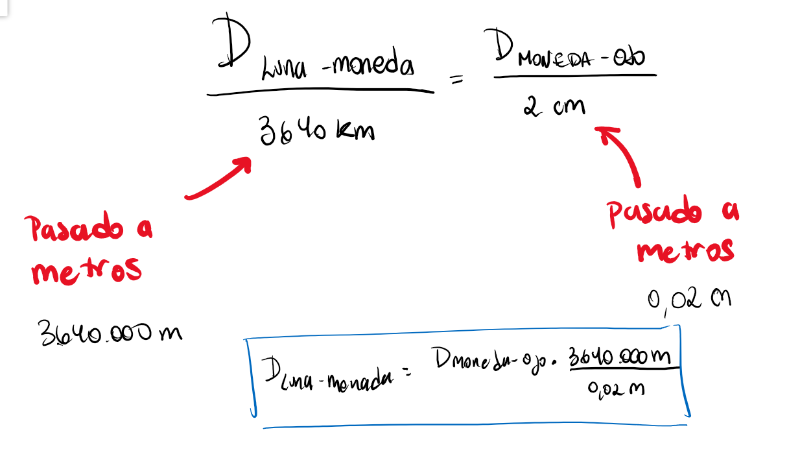
Realizar este experimento resulta algo tedioso, pero al final, se logra un método generalizado para calcular distancias a puntos lejanos. La distancia de la Tierra a la Luna es de 400.000 kilómetros. (aproximadamente)
El sextante

El sextante es un instrumento diseñado para poder realizar cómodamente estas mediciones, y fué esencial para aquellas personas que querían viajar lejos por mar.
Durante siglos se navegó siguiendo la costa utilizando como referencia sus puntos visibles y la profundidad de manera que cuando a finales del siglo XV los portugueses y castellanos comienzan sus viajes de exploración y descubrimiento, sus instrumentos de navegación eran la corredera y la ampolleta para determinar la velocidad del buque, imprescindible para navegación por estima; la sonda para determinar la profundidad y naturaleza del fondo; el compás que se orientaba al norte magnético, y el astrolabio y cuadrante para medir la altura de un astro sobre el horizonte.
El astrolabio se utilizaba para determinar la latitud mediante la observación de la estrella polar o la observación del paso meridiano del sol.
Se disponía de tablas que daban la declinación del sol para cada día del año y con esta información y la observación de la altura del sol en su paso meridiano era fácil determinar la latitud pero no había forma de determinar la longitud de modo que, en la práctica, el procedimiento seguido era el de navegar a un punto de la misma latitud que la del destino para luego ir navegando manteniendo la latitud hasta dar con el destino.
Alrededor de 1750 se inventó el sextante que permitía una observación mucho más precisa de la altura de los astros que con el astrolabio o el cuadrante.
Propuesta para hacer un sextante casero:
Este instrumento nos puede ayudar a determinar la altura de un mueble alto, para el cual no tengamos un instrumento de medición adecuado.
En primer lugar debemos crear una unidad de medida de longitud no convencional, para medir, en lugar de usar una cinta métrica, un instrumento láser, con algo que si tengamos a disponible cuando queremos realizar la medición.
(Podemos suponer el caso de estar varados en una isla tropical, y queremos medir la altura de un árbol)
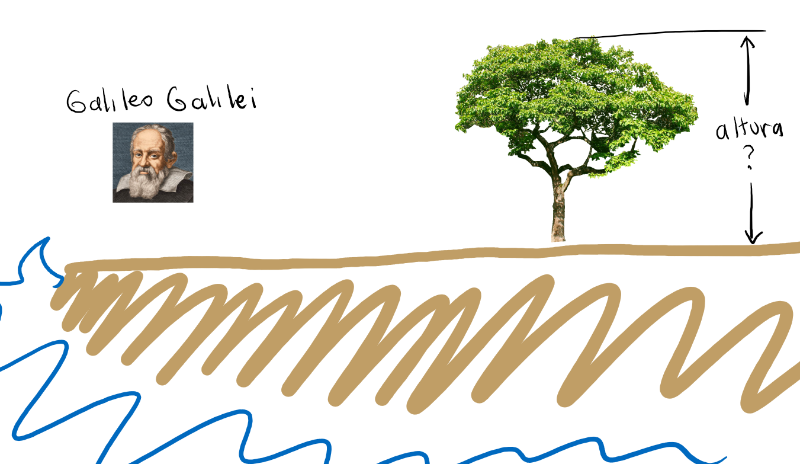
Un elemento que podemos tener a mano, o mejor dicho "a pié", es nuestro propio pié. La idea de medir con partes del cuerpo, no solo se ha registrado a lo largo del todo el mundo desde tiempos muy remotos, sino que fué un dato esencial para los cálculos de Eratóstenes para determinar el tamaño de la Tierra. Eratóstenes sabía que entre ambas columnas habían 5.000 pasos.
La unidad de medida, reconocida internacional mente como "pié" equivale a 24,5 centímetros. Pero tal vez nuestro pié, no mida eso. Lo importante entonces es determinar cuanto mide nuestro propio pié.

Luego debemos elegir un lugar desde donde realizaremos la medición. Desde ahí, realizaremos pasos de manera que nuestros piés siempre se toquen punta talón, y contar hasta llegar a la base del árbol.
Finalmente regresamos a nuestro lugar de medición. En él prepararemos nuestro instrumento de medición de la siguiente manera:
PROPUESTA PARA LA CASA
Inventar tu propia unidad de medida para la longitud, puede ser un dedo, una mano, un brazo, una pierna, un perro, objetos que te gusten. Proponé su nombre, si fuese que quisieras dedicarselo a una persona importante o científico, o tu propio nombre. Describí en qué situaciones podría llegar a ser más cómodo de emplear.
A partir de la teoría en la que está basado el sextante de tales, cuya ecuación es:
Empleá tu propia unidad de medida, para conocer la altura de un objetivo que te parece que puede ser medido. Te invito a registrar los pasos que realizaste, y documentar de manera escrita si te pareció que funciona correctamente o no, y que plantees cómo se te ocurre que podes mejorar tu unidad, o dispositivo sextante.