最短はDIJKだけ?
1。まずはダイクストラから
最短経路と言えばダイクストラ法
ダイクストラ法は隣接する範囲を1歩ずつ広げながら
各点への複数の経路を探索しながら
総コストの更新を続ける方法です。
ではアルゴリズムの方向性を知ろう。
まず、
グラフG(V,E)のスタートをsとします。
Vは頂点リスト、Eは辺ごとに(始点、終点、コスト)の3数組のリストにします。
直前の点uと、uの矢印の先の隣接点vの(u,v)組で調査を進めます。
未調査点UnReachは、はじめはVですが1点uからの全隣接点vを調査が終了するごとにuが削られます。
直前点uの先の隣接点vのdist(v)とvの直前点prev(v)を更新して進みますが、最初は∅で初期化します。
UnReach=∅になると探索は終わりです。
終わったときにVの各点xのdist(x)が最短距離になります。
目的点がeだとするとprev(prev(...prev(e)..))=sになるまで逆読みすれば最短経路になりますね。
どのデータを、どのように更新するか?
(出発点をsで初期化)
u=sなので、dist(s)=0, UnReach={a,b,c,d,e}です。v∈UnReachの全点に対して、dist(v)=∞とします。
(隣接点に進む)
・今uにいるとしましょう。uに隣接する各点v∈UnReachについて, コスト比較をします。
dist(v)=min(dist(v), dist(u) + cost(u,v)) でdist(v)は更新されるか温存が決まります。
現在のdist(v)を温存するならprev(v)も温存し、u経由が近ければ prev(v)=[u]と更新します。
・uから行ける隣接点vの全調査が終わるたびに、最小のv=vminを選び到達点を更新します。つまり、
UnReach=UnReach - {vmin} 、u=vmin
UnReach=∅となるまで(1辺進む)を続けます。
例を使って確認しましょう。
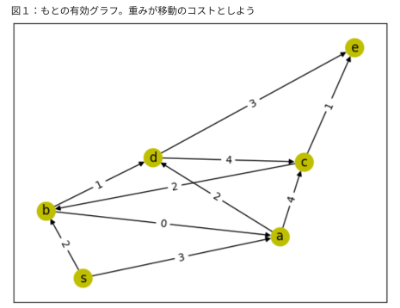
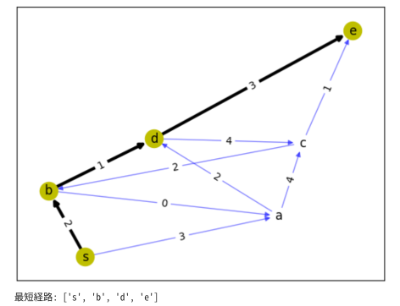
・頂点数7のグラフG(V,E)のスタートをsグラフ全体の頂点V=[s,a,b,c,d,e]
E=[ ("s","a", {'cost':3}),("s","b", {'cost': 2}),("a","C", {'cost': 4}),("a","d", {'cost' : 2}),
("b","a", {'cost': 0}),("b","d", {'cost': 1}),
("c","b", {'cost':2}),("c","e",{'cost': 1}),("d","c", {'cost': 4}),("d","e", {'cost': 3})]
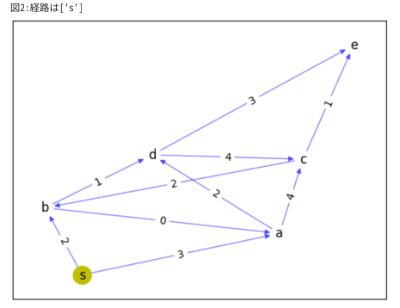
(s隣接のaに進む)
・u=sの先の1つv=a∈UnReach={a,b,c,d,e}について,
dist(a)=min(dist(a), dist(s)+d(s,a)) = min(∞,0+3)=3に更新され,prev(a)={ s }
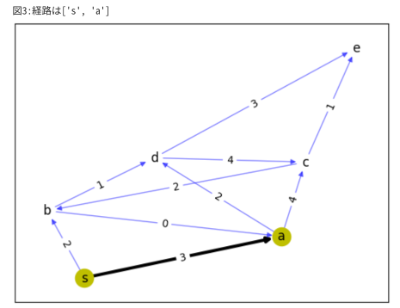
(s隣接のbに進む)
・u=aの1つ先のもう一つv=b∈UnReach={a,b,c,d,e}について,
dist(b)=min(dist(b), dist(s)+d(s,b)) = min(∞,0+2)=2でprev(b)={ s }
sの隣接点についてv=a,bではmin(f(a),f(b))=min(3,2)=2だから、vmin=b
・bは通過済なので、UnReach=UnReach - {b}={a,c,d,e}, ここで直前点の更新をしよう。u=b
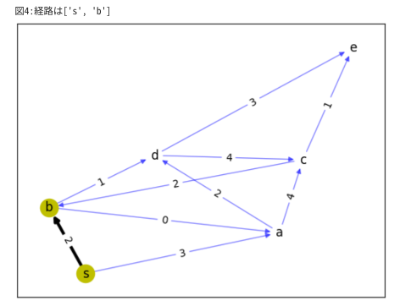
(b隣接のaに進む)
・u=b 1つ先v=a,d∈UnReach={a,c,d,e}について探索
dist(a) = min(3,2+0)=2に更新されます。
b経由が近いからprev(a)={ b }に更新。
dist(d) = min(∞,2+1)=3に更新されます。
b経由が近いからprev(d)={ b }に更新。
v=a,dではmin(f(a),f(d))=min(2,3)=2だから、vmin=a
・aは通過済なので、UnReach=UnReach-{a}={c,d,e}, u=a
(a隣接のc,dに進む)
・u=a 1つ先v=c,d∈UnReach={c,d,e}について探索
dist(c)= min(∞,2+4)=6に更新されます。
a経由が近いからprev(c)={ a }に更新。
dist(d)= min(3,2+2)=3で変わらず。
d直が近いからprev(d)=[b]のまま。
v=c,dではmin(f(c),f(d))=min(6,3)=3だから、vmin=d
・dは通過済なので、UnReach=UnReach- {d}={c,e}, u=d
(d隣接のc,eに進む)
・u=dの1つ先v=c,e∈UnReach={c,e}について探索
dist(c)= min(6,3+4)=6のまま。prev(c)={ a }のまま。
dist(e)= min(∞,3+3)=6に更新されます。
d経由が近いからprev(e)={ d }に更新。
v=c,eではmin(f(c),f(e))=min(6,6)=6だから差がない。vmin={c,e}
このあとc→e や e→cに進んでもコストがd(c,e)=1増える経路になるからその探索は
dist(c),dist(e)の更新にはつながらない。
・c,eは通過済なので、UnReach=UnReach-{c,e}=∅で終了。
最終更新を確認すると、
distは、a:2, b:2, c:6,d:6,e:6
prevは、a:b, b:s,d:b, c: a, e:d
だから、最短経路はs->b->a->c, s->b->d->eの2系統があることがわかるね。
質問:ダイクストラ法で最短経路を調べるコードはどう書けばよいでしょうか。
Pythonにはnx.dijkstra_path(G, start, goal,weight='重みの名前')という関数がありますから、それを使いましょう。start=s , goal=eとなるように関数に渡すと、最短経路となる頂点リスト ['s', 'b', 'd', 'e']を返して
もらいます。
#データ作成のみ
from matplotlib import pyplot as plt
import networkx as nx
def Dijkstra(V,E):
G = nx.DiGraph()
G.add_nodes_from(V)
G.add_edges_from(E)
start = V[0]
goal = V[-1]
dkV = nx.dijkstra_path(G, start, goal,weight='cost')
return dkV
V = ["s","a","b","c","d","e"]
E=[ ("s","a", {'cost':3}),("s","b", {'cost': 2}),("a","c", {'cost': 4}),("a","d", {'cost' : 2}),
("b","a", {'cost': 0}),("b","d", {'cost': 1}),("c","b", {'cost':2}),("c","e",{'cost': 1}),("d","c", {'cost': 4}),("d","e", {'cost': 3})]
print("最短経路:", Dijkstra(V,E))
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
[OUT]最短経路: ['s', 'b', 'd', 'e']
2.ダイクストラ法を実装しよう
質問:ダイクストラ法の中身を自分なりに作るにはどうしたらよいでしょう。
今度は最短経路リストをみつけるアルゴリズムを実装することに挑戦してみよう。
2つの辞書dist{点名:cost}, prev{点名:点名}と1つの集合UnReach{点名}
をダイクストラ法のルールで更新を続けて、到達点が∅になったら終了する。
最後に残った点までの距離に差がないと、永遠に続いてしまうために複数が最小になったら、
両方とも到達したことにする方法がある。
更新した辞書prevを終わりから読み取ってから逆順にすることでmy最短経路を見つけよう。
そして、networkxの関数nx.dijkstra_pathの結果と見比べよう。
#[IN]Python
#===========================================================
#重みつきのダイクストラ法の実装にチャレンジ(途中経過つき)
import networkx as nx
from math import inf as inf
def myDIJK(V,E,s,g):
G = nx.DiGraph()
G.add_nodes_from(V)
G.add_edges_from(E)
UnReach = set(V)
dist={}
prev={}
for item in UnReach:
dist[item]=inf
prev[item]=None
dist[s] = 0
u=s
UnReach -= set([u])
while len(UnReach)>0:
print("*UnReach",UnReach)
vs=list(G.successors(u))
print(f" u = {u}:vs = {vs}",end=" ,")
v_dists={}
for v in vs:
print(f"uv = {u}->{v}",end=" ,")
from_uv = dist[u] + G[u][v]['cost']
if dist[v]> from_uv:
prev[v]= u
dist[v] = min(dist[v], from_uv)
v_dists[v] = dist[v]
# 最小値のキーをタプルで取得
dist_min = min(v_dists.items(), key=lambda x: x[1])
v_mins = [key for key, value in v_dists.items() if value == dist_min[1]]
print(f"近い点 = {v_mins}")
u = v_mins[0]
UnReach -= set(v_mins)
print(f" prev = {prev}")
print(f" dist = {dist}")
print("*UnReach",UnReach)
conne = [g]
curr = g
while curr!= s:
curr = prev[curr]
conne.append(curr)
print(f"my最短経路={list(reversed(conne))}")
dkV = nx.dijkstra_path(G,s,g,weight='cost')
return dkV
V = ["s","a","b","c","d","e"]
E=[("s","a", {'cost':3}),("s","b", {'cost': 2}),("a","c", {'cost': 4}),("a","d", {'cost' : 2}),("b","a", {'cost': 0}),("b","d", {'cost': 1}), ("c","b", {'cost':2}),("c","e",{'cost': 1}),("d","c", {'cost': 4}),("d","e", {'cost': 3})]
print("最短経路:", myDIJK(V,E,"s","e"))
#========================================
[OUT]
*UnReach {'c', 'd', 'b', 'e', 'a'}
u = s:vs = ['a', 'b'] ,uv = s->a ,uv = s->b ,近い点 = ['b']
prev = {'s': None, 'c': None, 'd': None, 'b': 's', 'e': None, 'a': 's'}
dist = {'s': 0, 'c': inf, 'd': inf, 'b': 2, 'e': inf, 'a': 3}
*UnReach {'c', 'd', 'e', 'a'}
u = b:vs = ['a', 'd'] ,uv = b->a ,uv = b->d ,近い点 = ['a']
prev = {'s': None, 'c': None, 'd': 'b', 'b': 's', 'e': None, 'a': 'b'}
dist = {'s': 0, 'c': inf, 'd': 3, 'b': 2, 'e': inf, 'a': 2}
*UnReach {'c', 'd', 'e'}
u = a:vs = ['c', 'd'] ,uv = a->c ,uv = a->d ,近い点 = ['d']
prev = {'s': None, 'c': 'a', 'd': 'b', 'b': 's', 'e': None, 'a': 'b'}
dist = {'s': 0, 'c': 6, 'd': 3, 'b': 2, 'e': inf, 'a': 2}
*UnReach {'c', 'e'}
u = d:vs = ['c', 'e'] ,uv = d->c ,uv = d->e ,近い点 = ['c', 'e']
prev = {'s': None, 'c': 'a', 'd': 'b', 'b': 's', 'e': 'd', 'a': 'b'}
dist = {'s': 0, 'c': 6, 'd': 3, 'b': 2, 'e': 6, 'a': 2}
*UnReach set()
my最短経路=['s', 'b', 'd', 'e']
最短経路: ['s', 'b', 'd', 'e']
3。floyd-warshall法
最短経路を求めるには他の方法がいろいろあるようです。
たとえば、floyd-warshall法。
これを使うと、重みが負の数でも対応できて、計算時間も節約できる場合もあります。
使い方は簡単。
#[IN]Python
#=============================
import numpy as np
G = nx.DiGraph()
E=[("s","a", 3),("s","b", 2),("a","c", 4),("a","d", 2),("b","a", 0),("b","d", 1),("c","b", 2),("c","e",1),("d","c", 4),("d","e", 3)]
G.add_weighted_edges_from(E)
nx.floyd_warshall_numpy(G)
#=============================
[OUT]
array(
[[ 0., 2., 2., 6., 3., 6.],
[inf, 0., 6., 4., 2., 5.],
[inf, 0., 0., 4., 1., 4.],
[inf, 2., 2., 0., 3., 1.],
[inf, 6., 6., 4., 0., 3.],
[inf, inf, inf, inf, inf, 0.]])
入力は辺データを与えるだけで、
出力は各点から各点への最短の重みの合計を出してくれる。
すばらしい!
どのようなアルゴリズムなのだろうか?
連結を調べるときに連結行列の積を繰り返すことで、範囲を広げながら連結状態をしらべたね。
一斉に回数は1増やすことで、k番目からk+1番目の状態がわかりました。
これが動的計画法の発想です。
floyd_warshallは、動的計画法の考え方を使います。
初期化では、移動0のときのコスト行列Distを作ります。点viから点vjに移動するときのコストを設定します。i=jのときは0で、それ以外は∞にしておき、辺のデータEに合わせてコストを書き込みます。
次は、動的計画法(数学的帰納法、漸化式などのようにk番目からk+1番目を計算する)の実行です。
k番目のときの3つのコストDist(i,j),Dist(i,k),Dist(k,j)が求められたとしましょう。
そこで、点viから点vjに移動するコストが移動数を1増やしたとき、
k番目の点を経由した方がコスト増加が抑えられるかどうかを調べます。
つまり、 k+1番目のDist(i,j)はmin(Dist(i,j), Dist(i,k)+Dist(k,j))に更新するのです。
三角不等式で直線で囲んだ三角形ikjでは、辺ijは辺ikと辺kjの和より小です。
しかし、Distは直線距離ではなく、折れ線、しかも重みつきの合計なので、
毎回チェックと更新が必要になるのです。
この作業を、i行j列の行列の各数値n2個について実行します。
kを0からn-1までn回更新するので、計算個数はn3になりますね。
質問:floyd-warshall法を実装するにはどうしたらよいでしょう。
頂点数をnとするときn×nのコスト行列Distの初期化と、Distをn回更新します。
#[IN]Python
#=======================================
#重みつきのfloyd-warchall法の実装にチャレンジ
import networkx as nx
from math import inf as inf
def myFW(V,E):
G = nx.DiGraph()
# 数値だけのデータにして、重み合計の行列Distを作る。
dV={} # dV頂点名を0からの番号に訳す辞書。
numE=[] # numEは0からの頂点名にお置き換えられた辺データ。
for i,name in enumerate(V):
dV[name]=i
for item in E:
numE.append((dV[item[0]],dV[item[1]],item[2]))
G.add_weighted_edges_from(numE)
n = len(V)
Dist = [[inf]*n for i in range(n)] #距離行列Distは∞にする。
Dist = [[0 if i == j else Dist[i][j] for j in range(n)] for i in range(n)] #Distの対角成分を0にする。
# ここから、動的計画法の発想で、移動を1回ずつ増やした距離合計を最短にしながら更新する。
for k in range(n):
for u in range(n):
for v in range(n):
Dist[u][v] = min(Dist[u][v], Dist[u][k] + Dist[k][v])
print("my最短経路一覧")
print(Dist)
FWV=nx.floyd_warshall_numpy(G)
return FWV
#=======================================
V = ["s","a","b","c","d","e"]
E=[("s","a", 3),("s","b", 2),("a","c", 4),("a","d", 2),("b","a", 0),("b","d", 1),("c","b", 2),("c","e",1),("d","c", 4),("d","e", 3)]
print(f"最短経路表{myFW(V,E)}")
#=======================================
[OUT]
my最短経路一覧
[[0, 2, 2, 6, 3, 6], [inf, 0, 6, 4, 2, 5], [inf, 0, 0, 4, 1, 4], [inf, 2, 2, 0, 3, 1], [inf, 6, 6, 4, 0, 3], [inf, inf, inf, inf, inf, 0]]
最短経路表[[ 0. 2. 2. 6. 3. 6.]
[inf 0. 6. 4. 2. 5.]
[inf 0. 0. 4. 1. 4.]
[inf 2. 2. 0. 3. 1.]
[inf 6. 6. 4. 0. 3.]
[inf inf inf inf inf 0.]]