CAS: Lineare Gleichungssysteme konstruieren

Author:hawe

Arbeite im CAS mit Top-Down-Formeln

Änderungen der Eingangswerte sollen bis zum Ende durchrechnen
Eingeschränke Matrixmanipulation: Um Spalten zu bearbeiten muss für Zeilenoperationen transponiert werden mit abschließender (Rück) Transponierung (z.B: Spalte anfügen)

Eine Kupferlegierungen soll enthalten: 90% Kupfer, 5% Zink und 5% Zinn . Zur Auswahl stehen nun drei Legierungen A, B und C, die sich in der Zusammensetzung unterscheiden. Der Anteil dieser Größen in diesen Legierungen ist der nachfolgenden Tabelle zu entnehmen A B C Kupferanteil in % 80 95 80 Zinkanteil in % 20 0 10 Zinnanteil in % 0 5 10 a) Stelle ein LGS (konstante Werte auf rechte Seite setzen) auf, mit dem man entscheiden kann, ob sich die gewünschte Legierung aus den drei angebotenen zusammenschmelzen lässt. b) Bestimme die Lösungsmenge dieses LGS mit Hilfe des GAUSS-Verfahrens

Gauß-Elimination zur Dreiecks-Matrix R³ c) Welche Massen (in kg) der vorhandenen Legierungen müssen bestellt werden, um 5 Tonnen der gewünschten Legierung herstellen zu können? d) Angenommen, es werden jeweils 1000 kg von Legierung A und C sowie 5000 kg von Legierung B bestellt. Wie viel kg der gewünschten Legierung könnte man damit maximal produzieren? Und welchen Kupfer-, Zink-und Zinnanteil hat dann die Legierung, wenn man die Reste der Legierungen A und B zusammenmischen würde?

Codierung

Erstelle eine Hilffunktion für einen Gauß-Eliminationsschritt. Die LE-Matrix enthält die Spalte ss der Matrix AA dividiert durch Diagonal-Element ss - daüber 0en und darunter Vorzeichenwechsel: (1)LE(AA,ss):=Sequence(Sequence(If(j==ss ∧ k>ss,(If(k==ss,1,-1)*Element(AA,k,ss)/Element(AA,ss,ss)),((j==k)*1)),j,1,Length(AA)),k,1,Length(AA))

Zugabe Legierung A,B,C (2)X:={a,b,c} Gleichungen Cu-,Zi-,Zn-Anteil:

(3)GSO:={{80%a+95%b+80%c=90%(a+b+c)},{20%a+0%b+10%c=5%(a+b+c)},{0%a+5%b+10%c=5%(a+b+c)}}

Die Konstanten der rechten Seiten der Gleichungen schiebe ich in einen Vektor B (falls Variablen rechts stehen, setze die auf 0)

(4)B:=Transpose(Substitute(RightSide(Flatten(GSO)),X = Sequence(0,j,1,Length(X))))

Übertrage GSO in Matrix A₀ (dazu müssen alle Variablen der Gleichungen auf die linke Seite): Rechte Seite der Gleichungen von linker Seite abziehen:

(5)LGS:=B+Sequence(LeftSide(Element(GSO,j))-RightSide(Element(GSO,j)),j,1,Length(GSO))=0

Koeffizienten für a,b,c auslesen und mit B zusamenn in eine Matrix schreiben

(6)A_0:=Transpose(Join(Transpose(Substitute(Flatten(LeftSide(LGS)),X = Identity(Length(X)))),Transpose(B)))

Wenn der Algorithmus korrekt aufgebaut wurde, dann können wir die Bedingung c) in GSO ergänzen zu GSO:{{a+b+c=5000},{80% a + 95% b + 80% c = 90% (a+b+c)},{ 20% a + 0% b + 10% c = 5% (a+b+c)},{0% a + 5% b + 10% c = 5% (a+b+c)}} und die zusätzliche Gleichung sollte durchrechnen zu...

Gauß-Schritte im Bild mit 4. GLeichung a+b+c=5000

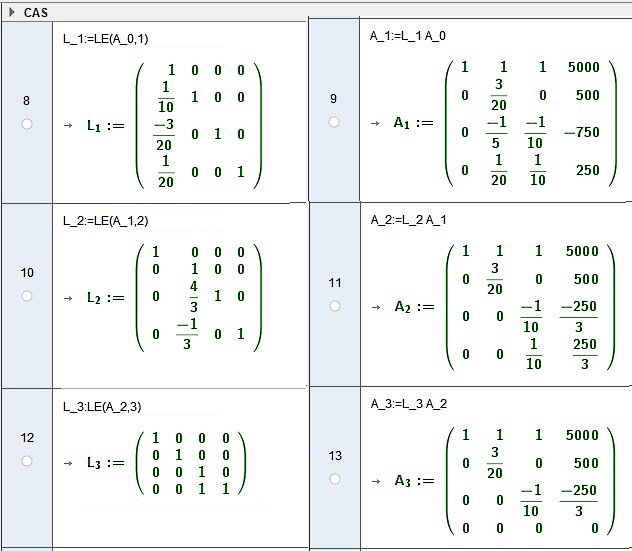
Allgemeine Gauß-Elimination zur Dreiecks-Matrix R³

Lösung der Dreiecksmatrix Zeile 3 ===> c Zeile 2 ===> b ===> in Zeile 1 ===> a


(14)Solve(A_3 Join(X,{-1}),X)

Mit 3 Gleichungen (ohne a+b+c=5000) erhalte ich (14)

d.h. d) c=1000 (15)Substitute($13,c = 1000)

Sum(RightSide(flatten($15)))

CAS: Lineare Gleichungssysteme konstruieren

Codierung

Gauß-Schritte im Bild mit 4. GLeichung a+b+c=5000

Allgemeine Gauß-Elimination zur Dreiecks-Matrix R³

Example

New Resources

Discover Resources

Discover Topics