Korrelaatio: tupakoijat
Monesti työelämässä ja "suuressa maailmassa" tahdotaan tietää, tai tahdotaan pystyä todistamaan, että jokin toivottu tai epätoivottu asia on "suoraa seurausta" jostakin toisesta asiasta. Esimerkiksi lääkefirma
tahtoo pystyä todistamaan tekemällään tutkimuksella, että heidän markkinoimansa lääke todella auttaa siihen vaivaan, johon sen väitetään auttavan.
Monesti myös tämänkaltaisia "havaintoja" tulkitaan pahasti väärin, ja senkin takia on hyvä tietää, mitä mahdollinen löytynyt korrelaatio tarkoittaa, ja mitä se välttämättä ei tarkoita. Jos lääkefirma väittää, että heitän masennuslääkettään syövät potilaat ovat selvästi vähemmän masentuneita, ja voivat osoittaa väitteensä tutkimuksin, on varmaankin turvallista vetää seuraava johtopäätös: lääkkeen syöminen vähentää masennusta.
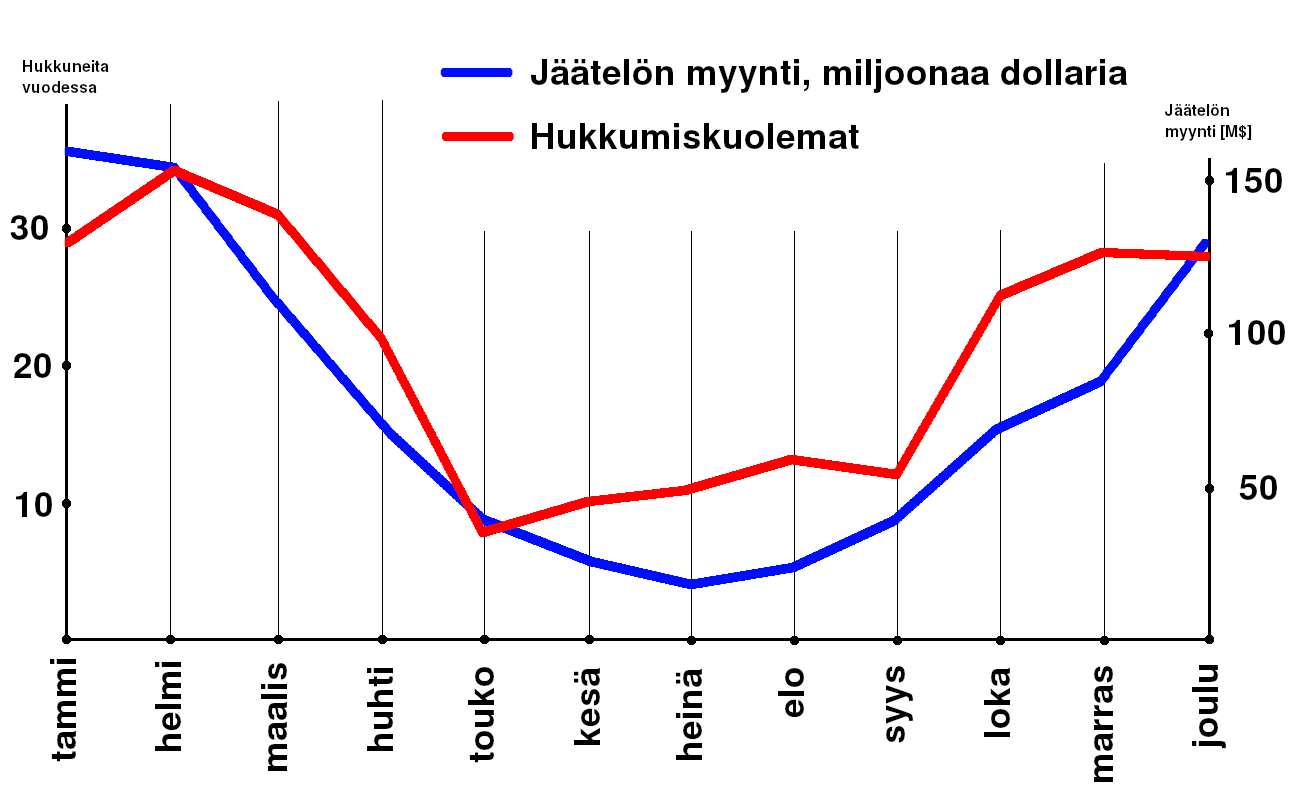
Maailma on kuitenkin myös täynnä ilmiöpareja jotka korreloivat, mutta joiden tapauksessa ei ole mielekästä väittä, että toinen aiheuttaisi toisen. Katsotaanpa alla näkyvää graafia: siinä on piirretty kuvaajat jäätelönmyynnin määrille ja hukkumiskuolemille ajan (kuukauden) funktiona eräältä vuodelta Australiasta. Ilman laskemistakin, jo kuvaa katsomalla, tämä ilmiöiden "käsi kädessä" kulkeminen on ilmiselvää: kun on paljon jäätelönmyyntiä, on paljon hukkumiskuolemia; toisaalta, kun on paljon hukkumiskuolemia, on paljon jäätelönsyöntiä. Koska valittu tapaus on niin ilmiselvä, kukaan ei tule väittämään, että jäätelönsyönti AIHEUTTAA hukkumiskuolemia, tai vastaavasti, että hukkumiskuolemat AIHEUTTAISIVAT jäätelönsyöntiä. Ilmiöt korreloivat, mutta kumpikaan ei aiheuta toista. Maailma on täynnä virheellistä uutisointia siitä, että jonkin asian väitetään aiheuttavan jotakin muuta vain sillä argumentilla, että ilmiöt korreloivat. Monesti voi kuitenkin olla niin, että korreloivat ilmiöt seuraavat jotakin yhteistä vaikutinta, tässä tapauksessa kuukauden keskilämpötilaa.
Toisena hyvänä esimerkkinä korreloivista, mutta tuskin toinen toisistaan johtuvista ilmiöistä mainittakoon ratsastusharrastuksen ja hyvän yleisen terveyden välinen korralaatio Amerikassa. Ratsastus on kallis harrastus johon on varaa vain rikkailla, ja samaisilla rikkailla on varaa hyvään terveydenhuoltoon. Vastoin kuin Suomessa, ei USA:ssa ole ilmaista terveydenhuoltoa.
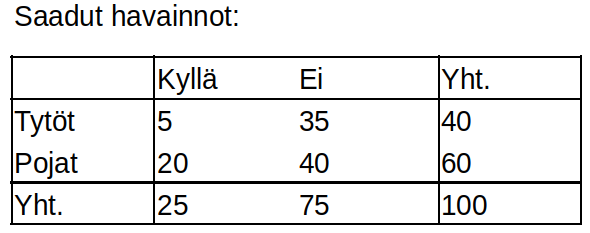
Siirrytään näiden esittelyjen jälkeen itse tapausesimerkkiin. Taulukossa alla on esitelty erään kyselytutkimuksen tulokset. Kyselyssä kysyttiin erään ammattikoulun oppilailta kaksi suoraviivaista kysymystä: oppilaan sukupuoli, vastaus kysymykseen "tupakoitko?". Kyselyllä haluttiin selvittää tupakoinnin mahdollista riippuvuutta (eli korrelaatiota) oppilaan sukupuolesta; eli siis sitä, onko tupakointi prosentuaalisesti yleisempää toisella ryhmällä kuin toisella. Tämä esimerkki on fiktiivinen, ja sen takia luvut on voitu valita niin, että tapaus on mahdollisimman helppo mieltää, ja toimii näin ollen esimerkkinä mahdollisimman hyvin. Käymme todellisuuteen pohjautuvan, mutta muuten vastaavan esimerkin seuraavana.

Ensimmäinen kysymys toki kuuluu, että kuinka tätä numeerista dataa pitäisi lähteä käsittelemään. Äkkiseltään näyttäisi, että pojista polttaa puolet, tytöistä vain yksi seitsemäsosa. Todennäköisyyslaskennassa meitä kiinnostaa kuitenkin tietää, mikä on se todennäköisyys, että saamme tälläisen tuloksen vain sattumalta, vaikka mitään korrelaatiota ei olekaan. Näin ollen, meidän täytyy ensin "luoda" luvut, jotka edustaisivat tätä oletettua todellisuutta; siis sitä, että korrelaatiota ei ole, ja tupakoijien määrät jakautuvat vailla sukupuolittumista. Näiden lukujen laskemista varten laajennamme saatujen tuloksien taulukkoa hieman. Laskemme yksinkertaisest yhteen tupakoijien/tupakoimattomien määrät, samoin tyttöjen/poikien määrät.
Tästä taulukosta voimme päätellä, että 25% oppilaista tupakoi, 75% ei tupakoi. Tutkmuksen piirissä oli 40 tyttöä. Jos mitään korrelaatiota ei olisi, tytöistä polttaisi 25%, eli 40*0.25 = 10. Kirjoitamme siis alla näkyvään taulukkoon polttavien tyttöjen määräksi 10. Vastaavasti 75% ei polta, joten kirjoitamme tupakoimattomien tyttöjen määräksi 40*0.75 = 30. Täysin vastaavasti, poikien määrä tutkimuksessa oli 60, joten tupakoivien poikien määräksi kirjoitetaan 60*0.25 = 15 ja tupakoimattomien poikien määräksi 60*0.75 = 45.

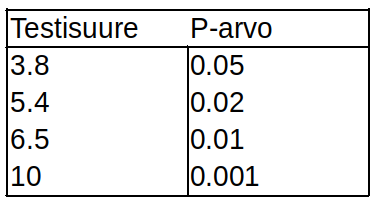
Seuraava vaihe on laskea testisuureen suuruus, ja verrata saatua arvoa taulukoituihin arvoihin. Mitä suurempi on testisuureen arvo, sitä suurempi on ilmiöiden välinen korrelaatio. Listaan on kirjattu muutama testisuureen arvo, ja sitä vastaava p-arvo. Tämä "p-arvo" on tilastomatematiikan käsite, josta on puhuttukin jo aiemmin: p-arvo tarkoittaa yksinkertaisesti sitä todennäköisyyttä, että tämä tulos olisi saatu sattumalta (ilman todelista korrelaatiota). Esimerkiksi p=0.01 tarkoittaisi siis sitä, että tämä tulos voitaisiin saada silkkana sattumana yhden prosentin todennäköisyydellä.
Nyt lasketaan testisuureen arvo. Testisuure siis kuvastaa sitä, kuinka paljon havainnot poikkeavat tästä näistä oletetuista "korrelaatiota ei ole"-luvuista. Lasku näkyy alla, ja laskusta mainittakoon muutama sananen. Termejä laskusa on yhtä monta kuin on tutkittavia arvoja: tässä tapauksessa . Jokaisessa termissä on osoittajassa todellisuuden ja "ei korrelaaiota"-oletuksen ero korotettuna toiseen, ja nimittäjässä on tämä oletettu "ei korrelaatiota"-arvo. Termit lasketaan yhteen, ja siinäpä laskettu testisuure onkin. Testisuuretta nimitetään tässä testissä nimellä ("Chi toiseen"). Miksi testisuureella on tämä nimi ja mistä se tulee, menee syvemmälle todennäköisyysteoriaan, ja siitä ei tarvitse tällä erää murehtia enempää.
Nyt, kun testisuure on laskettu, vertaamme sitä yllä esiteltyyn taulukkoon. Huomaamme, että saatu tulos oltaisiin voitu saada pelkkänä sattumana noin 2 prosentin todennäköisyydellä. On siis syytä olettaa, että tupakointi todellakin korreloi sukupuolen mukaan, eli sattumanvaraisesti poimittu poika on paljon suuremmalla todennäköisyydellä tupakoija kuin sattumanvaraisesti poimittu tyttö.