Winkelhalbierende
In der euklidischen Ebene ist eine Winkelhalbierende zweier sich schneidenden Geraden eine Gerade, an welcher die beiden gegebenen Geraden gespiegelt vertauscht werden. Es gibt immer zwei Winkelhalbierende; diese sind immer zueinander orthogonal. Die Spiegelung an einer Winkelhalbierenden in einem Dreieck vertauschen jeweils die beiden Seiten durch einen Eckpunkt und lassen diesen fest. Die beiden anderen Eckpunkte werden nur im Falle eines gleichschenkligen Dreiecks durch diese Spiegelung vertauscht.
Für zwei sich schneidende Kreise auf der Kugel gibt es genau zwei, zueinander orthogonale Winkelhalbierenden-Kreise durch die Schnittpunkte.
Die dazugehörigen Kreis-Spiegelungen vertauschen die beiden gegebenen Kreise.
Die gegenüberliegende Dreieck-Seite ist nur dann invariant, wenn der Winkelhalbierenden-Kreis orthogonal zu dieser Dreiecks-Seite ist.
(Siehe die Seite Symmetriekreise von 2 Kreisen).
Diese Seite ist eine Aktivität des geogebra-books kugel-dreiecke (August 2018)
Die Dreiecksseiten des obigen Kugeldreiecks sind Teile von 3 Kreisen. Zwei Kreise besitzen genau 2 zueinander orthogonale Kreise als Winkelhalbierende. Das Dreieck besitzt 6 Winkelhalbierende, die sich im besten Falle zu je dreien in 8 Punkten schneiden. Durch Veränderung der Lage der drei Kreise können jedoch auch ganz andere Bilder entstehen: man bewege die Dreieckspunkte (große grüne Punkte) und ändere die Kreise (kleine grünen Punkte). Die blauen Punkte legen die Dreiecksseiten fest.
Im Applet unten kann man die Möglichkeiten in der Ebene erkunden. Die Punkte A und B und der Kreis durch AB sind fix. Beweglich ist die Dreiecksecke C. Die Kreise durch A und C, bzw. durch B und C kann man mit den Punkten AC bzw. BC festlegen. Die Dreiecksseiten können sich in C berühren oder sich sogar zwischen den Eckpunkten überschneiden!! Dabei können Winkelhalbierenden-Schnittpunkte verschwinden oder zusammenfallen.
In der Regel liegen die Dreieckspunkte nicht symmetrisch zu den Winkelhalbierenden. Symmetrien liegen nur dann vor, wenn Winkelhalbierende orthogonal zur gegenüberliegenden Dreiecksseite liegen. Die zugehörigen Winkel sind dann gleich.
In der 3D-Ansicht kann man dies an dem 8-Eck aus den Winkelhalbierenden-Schnittpunkten auf der Kugel und ihren Diagonalen beobachten: bei Symmetrien liegen die zusammengehörenden Diagonalen in einer Ebene.
Winkelhalbierenden-Schnittpunkte: einige mögliche Fälle als Bilder
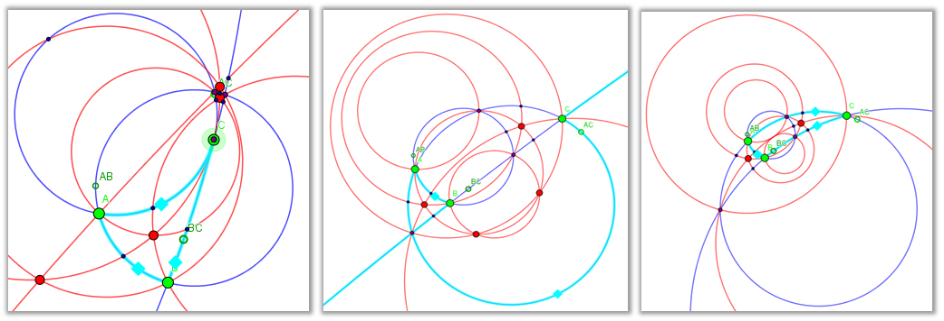
Symmetrieen
Ist eine Winkelhalbierende orthogonal zur gegenüberliegenden Dreiecks-Seite, so läßt die Spiegelung an der Winkelhalbierenden die gegenüberliegende Dreiecks-Seite invariant, die beiden Eckpunkte und die anliegenden Dreiecks-Seiten werden vertauscht.
Wir nennen in Analogie zu ebenen Dreiecken diese Kreisdreiecke gleichschenklig: zwei Seiten sind "isomorph" - sie werden durch eine Kreisinversion vertauscht.
Im Applet links unten kann man ausprobieren, welche Möglichkeiten hiebei auftreten können.
Die Punkte A, B und Mc sind fix, C läßt sich auf der Senkrechten bewegen, die Kreiswinkel werden durch AC beeinflusst.
Gleichschenklige Kreisdreiecke - - - - - - - - - - - - - Gleichwinklige Kreisdreiecke
Das Kugeldreieck unten ist besonders symmetrisch: es ist dreifach rechtwinklig: . Die Winkelhalbierenden-Schnittpunkte sind die Ecken eines Würfels, die Schnittpunkte der Dreiecksseiten-Kreise bilden ein Oktaeder. In den Winkelhalbierenden-Schnittpunkte schneiden sich die Winkelhalbierenden unter Vielfachen von 60°.
4 der Winkelhalbierenden-Schnittpunkte, geeignet gewählt, bilden einen Tetraeder. Je 3 der Tetraeder-Punkte bilden ein symmetrisches Kugeldreieck mit - Innenwinkeln.
Würfel, Oktaeder und Tetraeder
In obigem Applet ist der 3D-Mittelpunkt der Kugel auch der Mittelpunkt von Würfel, Okaeder und Tetraeder. Das erleichtert die Konstruktionen.
Es könnte aber auch jeder andere Punkt im Inneren der Kugel als Mittelpunkt der Figuren gewählt werden.
Da Möbiustransformationen kreis- und winkeltreu sind, ergäben sich isomorphe Bilder, jedoch nicht im euklidischen Sinne!